Процедура скользящего суммирования

Пусть

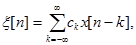(2.58)

где x[n] - нормальный дискретный «белый шум».

Тогда спектральная плотность процесса (2.58) на основе (2.51) имеет вид:

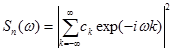(2.59)

Корреляционная функция процесса (2.58) определяется зави­симостью (2.47).

Считая известными значения корреляционной функции К_п(n) в достаточно большом диапазоне –р £ n £ p, можно найти с доста­точной точностью ее преобразование Фурье - спектральную плот­ность S_п(w), а затем разлагая корень из нее в ряд Фурье, найти коэффициенты с_k. Это дает возможность моделировать сам процесс с помощью соотношения:

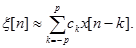(2.60)

Для моделирования начального значения нужно иметь 2р+1 нормальных случайных величин N(0,1), а для последующих - еще одно дополнительное случайное число.

Количество слагаемых в зависимости (2.60) зависит от тре­буемой точности и характеристик процесса и, как правило, не превосходит 5...10.

Нетрудно показать, что для СНСП, имеющего корреляци­онную функцию (2.39) и спектральную плотность, полученную в результате преобразования Фурье:

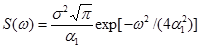(2.61)

коэффициенты определяются зависимостью:

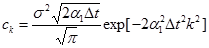. (2.62)

Для моделирования СНСП по рассмотренным алгоритмам необ­ходимо достаточно корректно определить шаг дискретизации (Dt). Для этого необходимо знать:

1. Интервал времени моделирования случайного процесса Т в секундах.

2. Интервал частот, в которых задана спектральная плот­ность - [-В; В] в герцах (ширину частотного спектра).

Тогда необходимое число равноотстоящих выборочных значе­ний последовательности без существенной потери информации оп­ределяется зависимостью:

n³ 2BT, (2.63)

а интервал дискретизации:

Dt = Т/n. (2.64)

Кроме того минимальный интервал времени моделирования и ошибка измерения основных характеристик случайного процесса (МОЖ, корреляционной функции, спектральной плотности) связаны равенством:

Т_min= (Be²)^-1, (2.65)

где e - погрешность измерения характеристик процесса.

Случайный процесс, протекающий в системе, называется мар­ковским, если для любого момента времени t₀ вероятностные ха­рактеристики процесса в будущем зависят только от его состоя­ния в данный момент времени и не зависят от того, когда и как система пришла в это состояние.

Марковские случайные процессы наибольшее применение нахо­дят при исследовании систем массового обслуживания, на которых поступает простейший поток заявок, т.е. стационарный, ординар­ный и не имеющий последействия. При этом хорошо известно, что интервал времени между соседними заявками имеет показа­тельное распределение.

Поэтому моделирование марковского случайного процесса сводится к моделированию моментов времени t_i, характеризующих временную последовательность поступления заявок, т.е. к моде­лированию случайных величин, имеющих показательное распределе­ние.