Алгоритмы проверки стационарности данных

1) Проверка гипотезы о стационарности объекта по средним значениям и дисперсиям измерений:

Дано:

Х={х1,…, 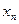}, где

n – измерение;

Разбиваем последовательность на две части:

Х1={x1,…, }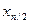

Х2={ ,…, }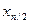

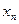Определяем среднее значение:

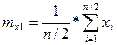
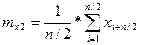
Сравниваем:

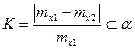
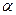- допустимая погрешность, уровень, .

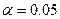Если это условие выполняется, то объект стационарный, а если не выполняется – то нестационарный. Аналогично и для дисперсии.

2) Проверка гипотезы о стационарности объекта по критерию серий Вальда-Вольфовица

Дано: выборка значений

Х={х1,…, 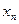}, где n – измерения;

Определяем медиану значений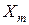

Для каждого сигнала вычисляем количество серий: серии последовательности «+» и «–»

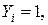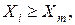
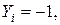если

если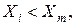

Определяем количество «+» и «–»

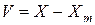
Сравниваем

If (V(i).*V(i-1)<0)

Если это условие выполняется, то количество серий увеличивается.

По табл. значениям определяем доверительные точки критерия серий.

Если 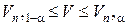, то объект стационарен по критерию серий.

3) Проверка нормальности закона распределения по t-критерию Стьюдента

Дано: выборка Х={х1,…, 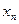}, где n – измерение;

1. Разбиваем последовательность на две части:

Х1={x1,…, }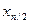

Х2={ ,…, }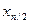

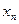2. Вычисляем среднее значение для всей выборки и для каждой из последовательностей.

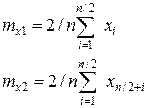
3. Определяем модуль разностей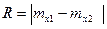

4. Определяем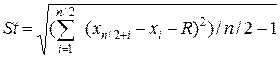

5. Вычисляем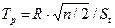

6. Сравниваем , если 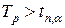– нормальный закон распределения, 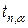выбирается из таблицы, где n – количество измерений, а 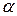– погрешность измерений.