Критерий Гурвица (критерий асимптотической устойчивости)

Дан характеристический полином:

Характеристическое уравнение:

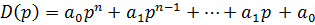
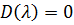
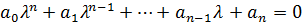-характеристическое уравнение n-мерной системы

Условие устойчивости:

-Необходимое условие: все коэффициенты характеристического уравнения должны быть положительными

-Достаточное условие: Все определители Гурвица 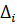должны быть положительными при i=1..n

Матрица Гурвица для системы n порядка:

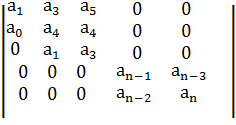, где определители Гурвица:

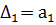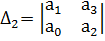, и т.д. Таких определителей всего n штук.

Примечание: если нет коэффициентов, то в соответствующий член матрицы равен нулю

Критерий устойчивости по Гурвицу

-Необходимое, но не достаточное условие: все коэффициенты характеристического уравнения должны быть положительными

-Достаточное условие: все определители Гурвица должны быть положительными.

Для систем 1 или 2 порядка необходимое условие является достаточным

Вычисление n-го определителя:

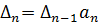
Для системы 3 порядка необходимо выполнение обоих условий:

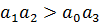
Для системы 4 порядка достаточным условием является:

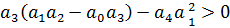
Границы устойчивости

Есть 3 типа границ устойчивости:

· когда 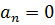-есть нулевой корень. При условии, что все остальные коэффициенты положительны, это называется апериодической границей устойчивости

· когда 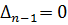-появляется пара чисто мнимых корней. При условии, что все остальные коэффициенты положительны, это называется колебательной границей устойчивости.

· когда есть бесконечно удаленный корень - возможно при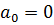

Если разделить характеристическое уравнение на 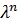, то получается:

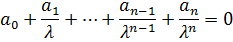
При 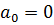корень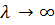

Доказательство необходимого условия:

Пусть все коэффициенты положительны, тогда характеристическое уравнение можно представить в следующем виде:

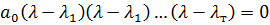
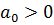
Пусть корни уравнения либо отрицательные действительные, либо комплексные с отрицательной действительной частью, тогда:

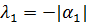
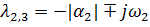
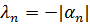
После подстановки этого в исходное уравнение получается:

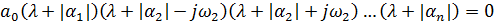
Комплексные сопряженные сокращаются:

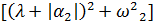[][]=0

Доказано, что все коэффициенты в случае устойчивой системы должны быть положительными

Пример. Необходимо определить, при каких параметрах данная система будет устойчива, и определить передаточную функцию замкнутой системы (см. Рис. 10.1).

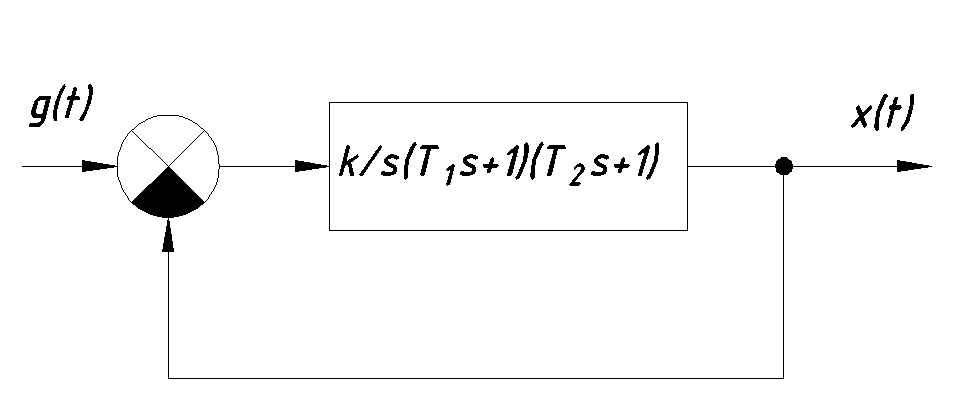
Рис. 10.1

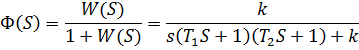
Характеристический полином:

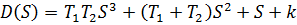
Обозначим: , , ,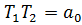

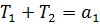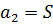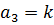
Матрица Гурвица:

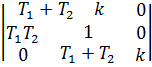
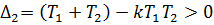
Условие устойчивости: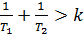

Границы устойчивости (см. Рис. 10.2, Рис. 10.3):

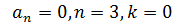- -апериодическая граница

-

- ,

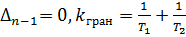
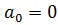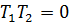
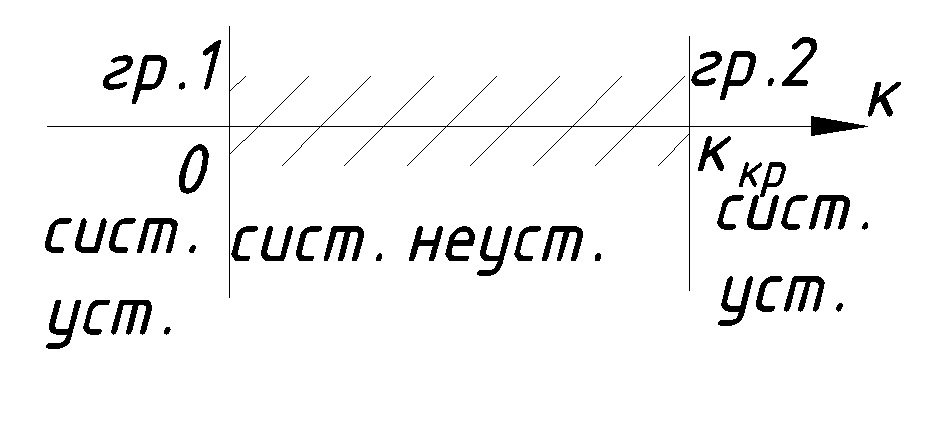
Рис. 10.2

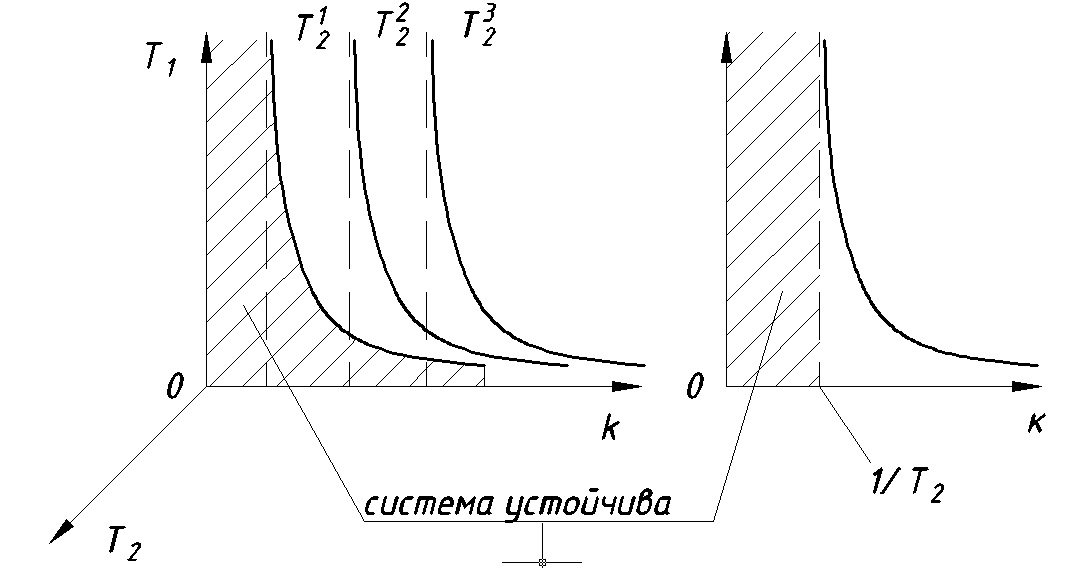
Рис. 10.3