Передаточные функции разомкнутых и замкнутых систем

Передаточная функция разомкнутой системы (Рис. 7.1):

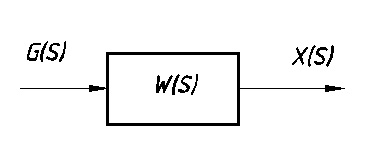
Рис. 7.1

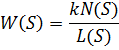
Примечание: звено называется интегрирующим, если в знаменателе есть в чистом виде S; если S в чистом виде находится в числителе, то звено называется дифференцирующим.

Дифференциальное уравнение системы в форме L:

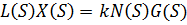
Передаточная функция системы при последовательном соединении звеньев (см. Рис. 7.2):

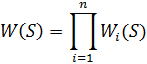
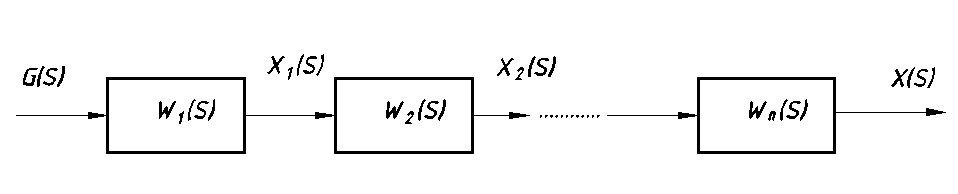
Рис. 7.2

Передаточная функция системы при параллельном соединении звеньев (см. Рис. 7.3):

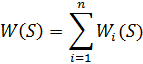
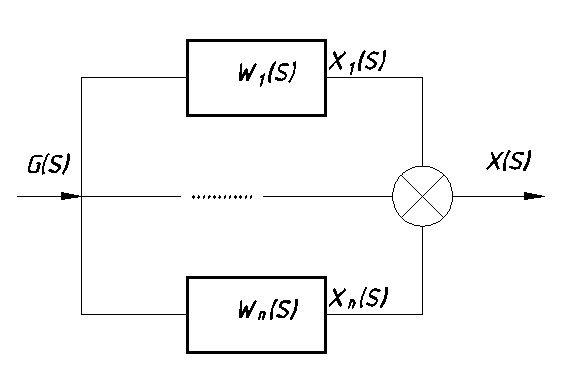
Рис. 7.3

Местная обратная связь:

Уравнение системы с обратной связью (см. Рис. 7.4):

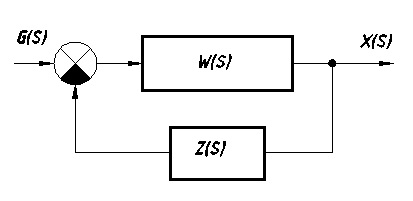
Рис. 7.4

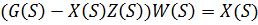
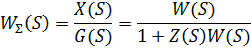
При единичной обратной связи:

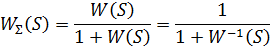
Примечание: далее W(S)-передаточная функция разомкнутой системы, Ф(S)-передаточная функция замкнутой системы. Передаточная функция замкнутой системы:

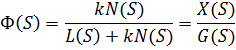
Характеристический полином замкнутой системы:

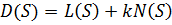
Характеристическое уравнение замкнутой системы:

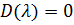
Характеристическое уравнение разомкнутой системы:

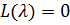
Передаточная функция по возмущающему воздействию:

Рассмотрим систему, изображенную на рис. 7.5.

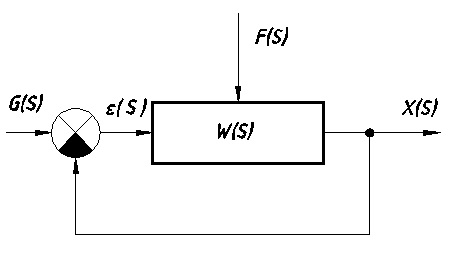
Рис. 7.5

Примечание:

· g(t)/G(S)-управляющее воздействие

· х(t)/Х(S)-регулируемая величина

· f(t)/F(S)-возмущающее воздействие

· ε(t)/ ε (S)-ошибка

Функция ошибки: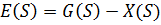

Передаточная функция по ошибке:

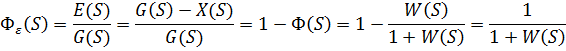
Преобразуем исходную схему с помощью правил структурных преобразований (см. Рис. 7.6):

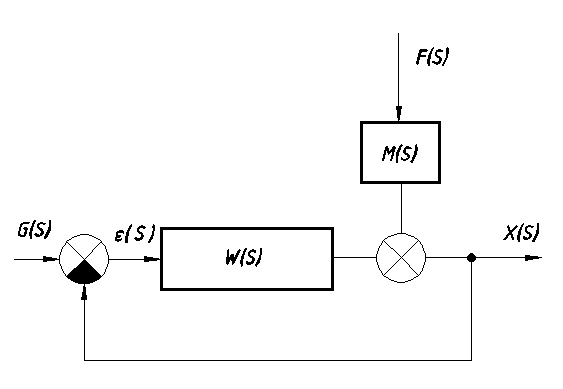
Рис. 7.6

Следовательно:

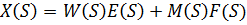
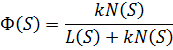
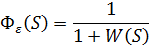
Значит, передаточная функция по возмущающему воздействию равна:

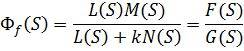
Примечание: порядок разомкнутой системы определяется по порядку замкнутой системы.

Основные уравнения следящих систем.

Дифференциальное уравнение системы (см. Рис.7.6):

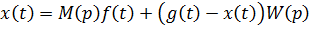
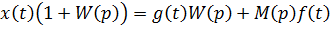
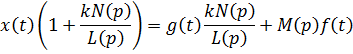
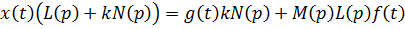
Обозначим: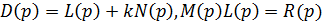

Дифференциальное уравнение замкнутой системы:

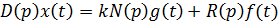
Дифференциальное уравнение по отклонению по ошибке:

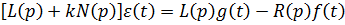
Дифференциальное уравнение системы в форме Коши при отсутствии возмущающих и входных воздействий:

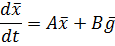
Данное уравнение определяет собственное движение системы

Характеристическое уравнение для данного ДУ:

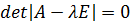, где Е - единичная матрица