Критерий устойчивости Найквиста

Данный критерий позволяет судить об устойчивости системы по виду передаточной функции разомкнутой системы. Обратная связь единичная отрицательная.

Возможны несколько вариантов: разомкнутая система может быть устойчивой или неустойчивой, может обладать астатизмом какого-то порядка.

►1.Система устойчива в разомкнутом состоянии.

Передаточная функция разомкнутой системы:

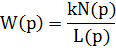
Передаточная функция замкнутой системы:

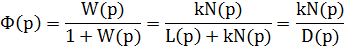
D(p) -характеристический полином

Вводится вспомогательная функция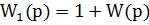

Передаточная функция: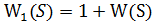

Далее для данной функции строится годограф. Для построения годографа S=jω:

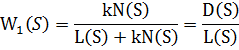
L(S)-характеристический полином разомкнутой системы

D(S)-характеристический полином замкнутой системы.

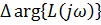-аргумент разомкнутой системы

По Михайлову: 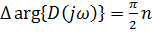, где n-порядок системы.

Если система устойчива в замкнутом состоянии, то:

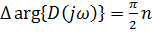(при изменении )

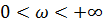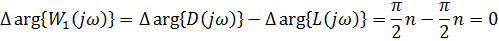
Годограф функции (Рис. 12.1) не должен охватывать начало координат, иначе угол изменится на 90°:

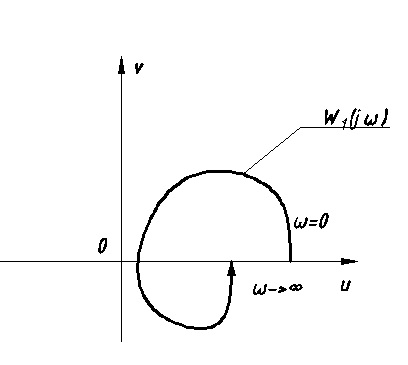
Рис. 12.1 Годограф функции

Тогда передаточная функция замкнутой системы равна:

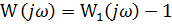
Соответствующий годограф изображен на Рис. 12.2

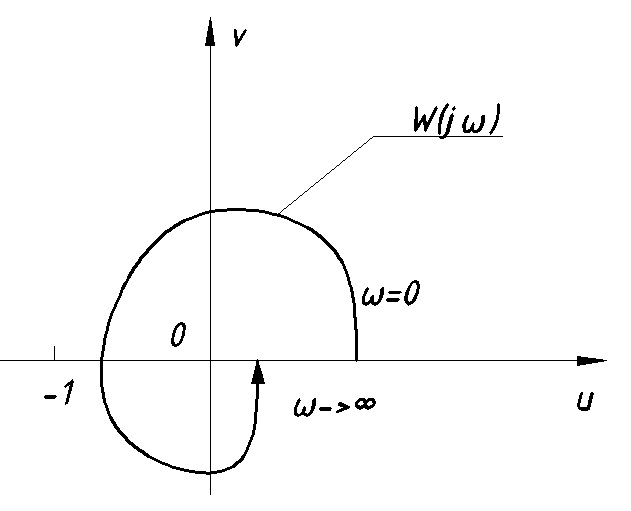
Рис. 12.2

Был получен годограф, смещенный на 1.

Чтобы САР была устойчивой в замкнутом состоянии, если она устойчива в разомкнутом состоянии, необходимо и достаточно, чтобы годограф разомкнутой системы не охватывал точку

(-1;j0) при изменении частоты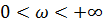

►Случай 2. Система неустойчива в разомкнутом состоянии

Если система неустойчива, то в правой полуплоскости есть m корней:

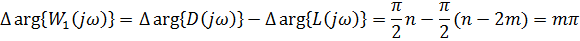
Для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф замкнутой функции охватывал точку (-1;j0) против часовой стрелки на угол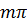

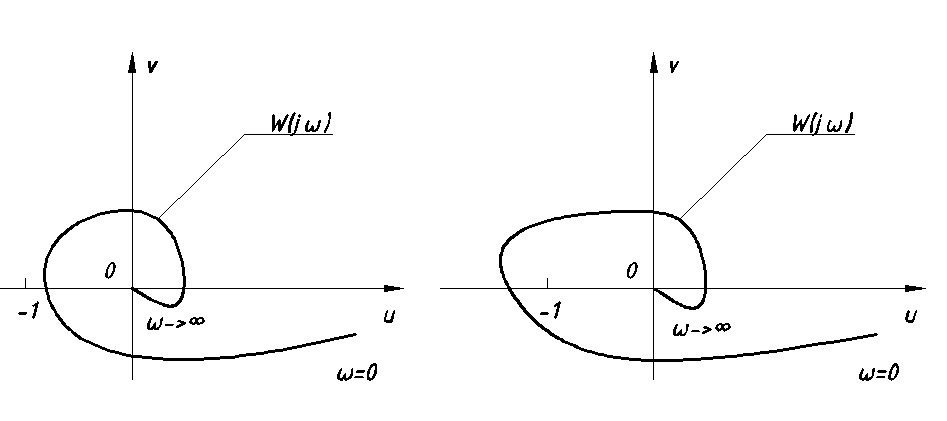
Рис. 12.3

Для неустойчивой в разомкнутом состоянии системы обычно сложно подсчитать количество охватов точки (-1;j0). Считается количество охватов в интервале (-∞,-1)

Определение: для того чтобы замкнутая система была устойчивой при неустойчивой разомкнутой системе, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов была больше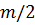

Примечание: если начальная точка годографа находится на действительной оси левее -1, то это считается за половину перехода.

Пример

m=1, система устойчива (Рис.12.4)

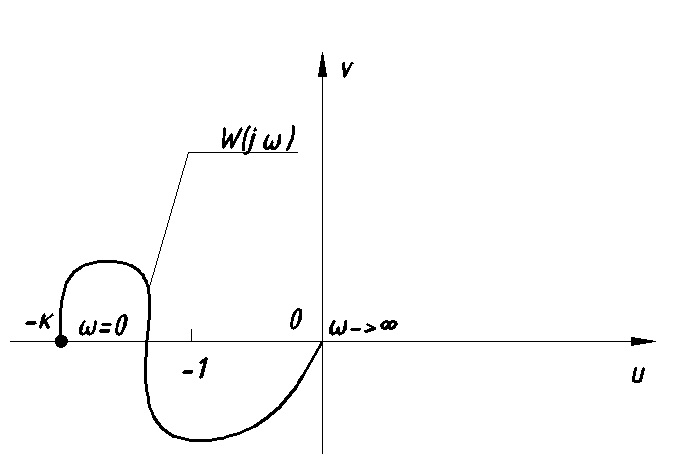
Рис.12.4 Система устойчива

m=3, система устойчива (Рис. 12.5)

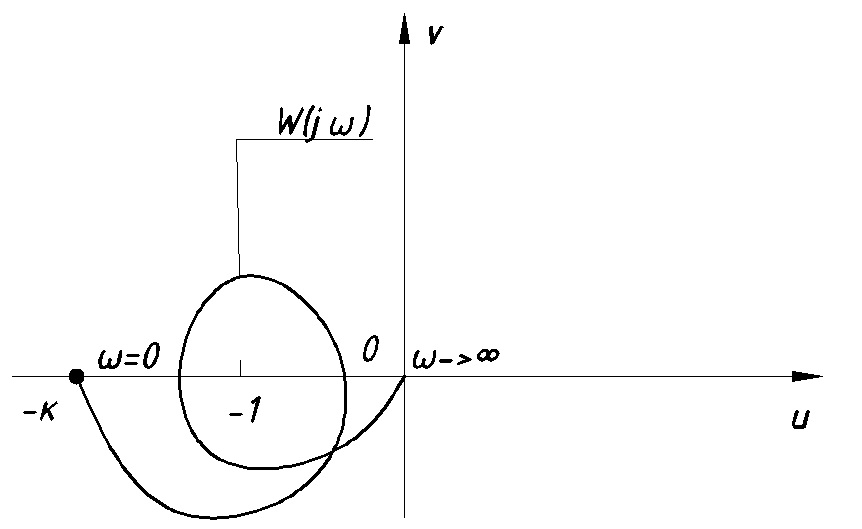
Рис. 12.5 Система устойчива

►Случай 3. Разомкнутая система является астатической (Рис. 12.6).

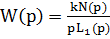-есть один нулевой полюс, это астатизм 1 порядка.

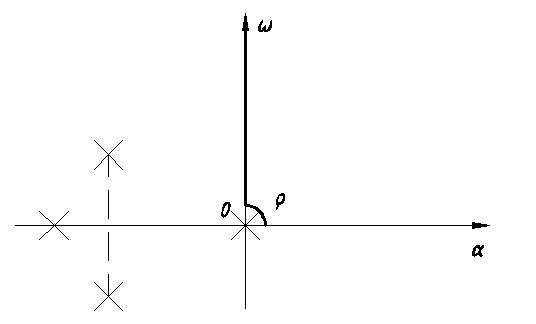
Рис. 12.6

Так как частота меняется от нуля до плюс бесконечности, то двигаемся вверх по мнимой оси.

Для того, чтобы все корни оставались слева, обойдем начало координат справа по окружности малого радиуса.

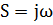-плоскость корней

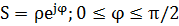
Тогда при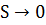

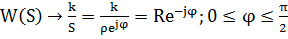
При 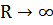получается бесконечно большой радиус

Строим годограф (Рис. 12.7):

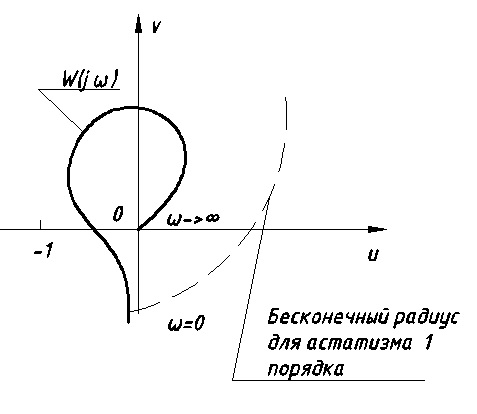
Рис. 12.7 Годограф

Получаем бесконечно большой радиус для астатизма 1 порядка. Значит, система устойчива, т.к. годограф не охватывает точку (-1;0j).

Астатизм 2 порядка (Рис. 12.8)

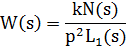
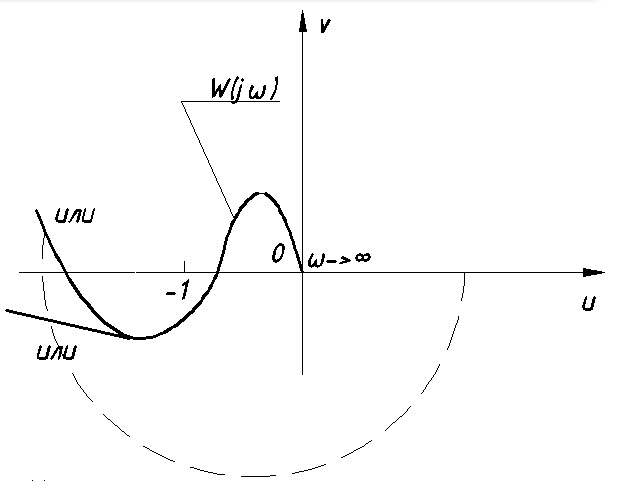
Рис. 12.8 Система устойчива

Здесь точка (-1;0j) не охвачена, значит система устойчива

Астатизм 3 порядка (Рис. 12.9)

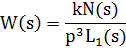
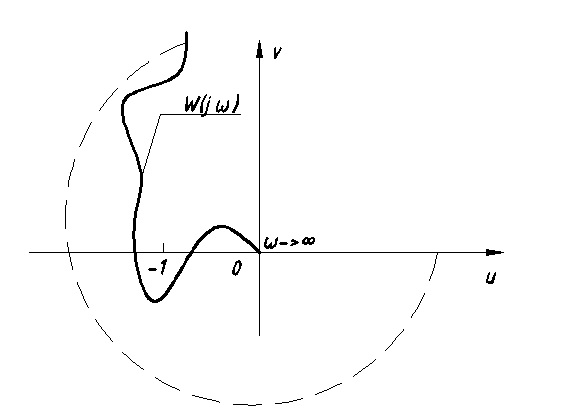
Рис. 12.9

Использование логарифмических характеристик для исследования устойчивости

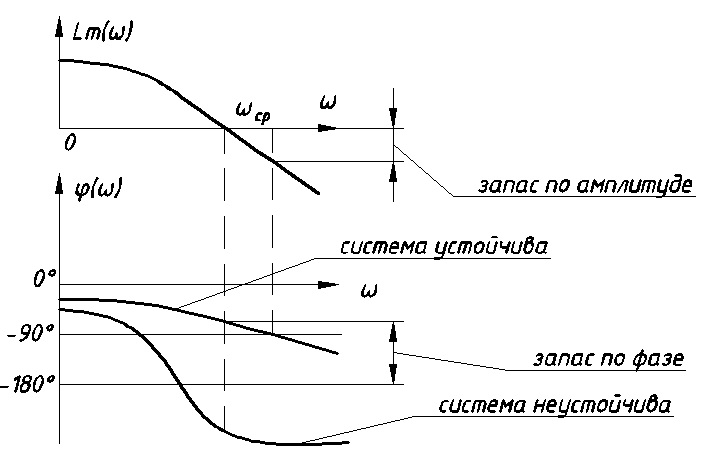
Рис. 12.10

Для определения запаса устойчивости по фазе, нужно измерить расстояние от ЛФЧХ при частоте среза до -180 градусов (см. Рис 12.10). Если система устойчива, то:

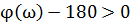
На практике часто требуется запас по фазе > 45 градусов

Для определения запаса по амплитуде необходимо для точки, где ЛФЧХ равна нулю, определить расстояние от ЛАЧХ до оси абсцисс - ЛАЧХ должна в точке этой под осью абсцисс быть (см. Рис. 21).

На практике часто требуется запас по амплитуде > 12 дБ