2015-05-12
707
Данный критерий позволяет определить устойчивость системы по виду характеристического уравнения замкнутой системы с помощью частотных характеристик.
Характеристический полином:
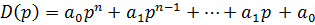
Корни характеристического уравнения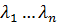 
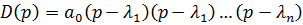
Далее строится годограф (см. Рис. 11.1):
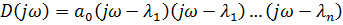
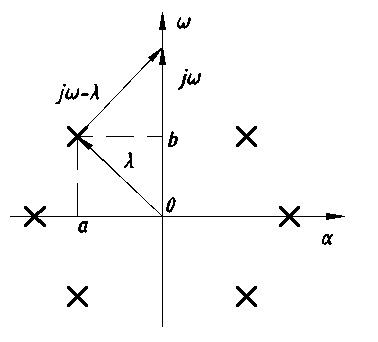
Рис.11.1 Плоскость корней характеристического уравнения
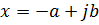
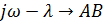
Рассматривается левый корень:
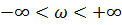
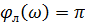
Для правых корней:
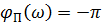
При изменении частоты 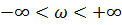получаем аргумент:
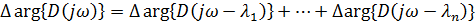
Пусть есть n корней, из которых m-в правой полуплоскости
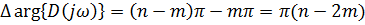
При изменении частоты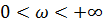 
получаем аргумент:
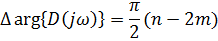
Для устойчивости системы не должно быть корней в правой полуплоскости: m=0
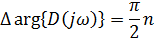
Критерий Михайлова-годограф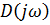 
-кривая Михайлова - симметрична относительно действительной оси.
Отрицательные частоты не рассматриваются. Пусть дана система n порядка
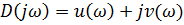,где
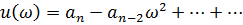
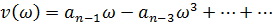
При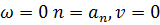 
-начальная точка кривой Михайлова
При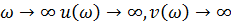 
Для устойчивости линейной системы порядка n необходимо и достаточно, чтобы кривая Михайлова начиналась на действительной оси и последовательно охватывала n квадрантов против часовой стрелки, при этом все время окружая начало координат (См. Рис. 11.2).
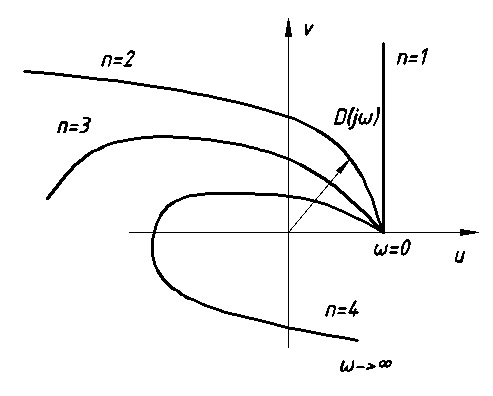
Рис.11.2 данные системы устойчивы
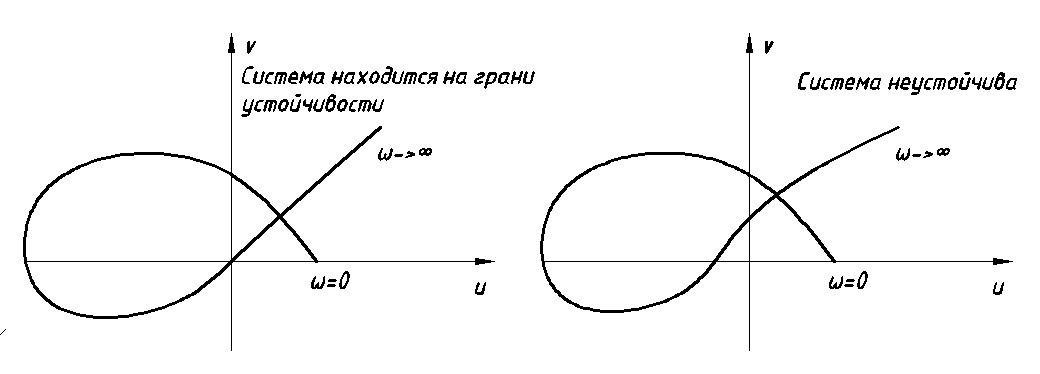
Рис. 11.3
В данном случае система неустойчива (рис.11.3, справа), так как есть корни в правой полуплоскости.
Другая форма критерия Михайлова
Эта форма состоит в том, что корни характеристического уравнения перемежаются один за другим от точки, где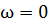 
до точки, где 
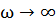(Рис.11.4). Мнимая и действительная оси должны попеременно пересекаться.
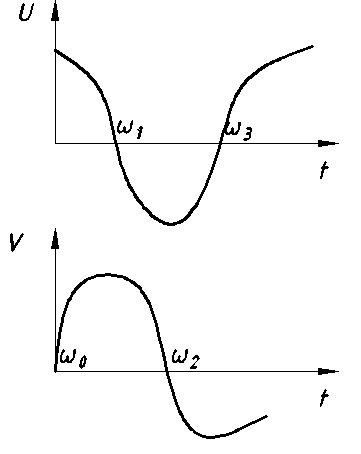
Рис. 11.4 Другая форма критерия Михайлова
