у' = f 1(x)× f 2(y).
Решение.
dy/dx = f 1(x)× f 2(y) |× dx / f 2(y), f 2(y) ≠ 0,
dy/ f 2(y) = f 1(x)× dx,
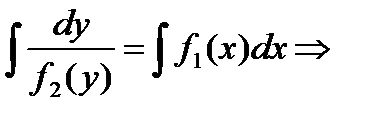 общее решение (общий интеграл) уравнения.
общее решение (общий интеграл) уравнения.
Случай f 2(y) = 0 рассматривается с помощью подстановки в исходное уравнение.
Пример 2.11. Решить уравнение 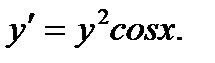
Решение.
dy/dx = у 2 сosx |× dx / у 2, у ≠ 0,
dy / у 2 = cosxdx,
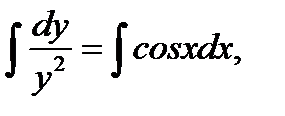
–1/ y = sinx + C,
y = –1/(sinx + C) – общее решение.
Рассмотрим случай у = 0.
Подставляя в исходное уравнение у = 0, получаем:
0' = 02 cosx, 0 = 0 – верно Þ у = 0 – решение уравнения.
Это решение не может быть получено как частное решение общего решения ни при каком значении С.
Ответ: y = –1/(sinx + C), у = 0.
2.81. Решить уравнения:
1) 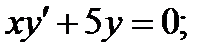 2)
2) 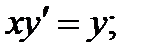 3)
3) 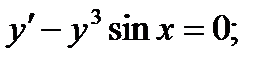
4) 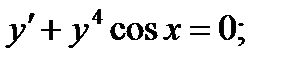 5)
5) 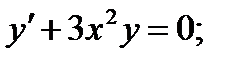 6)
6) 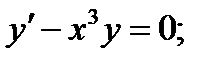
7) 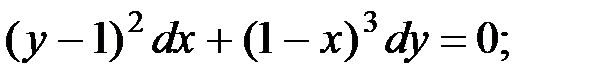 8)
8) 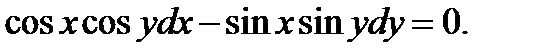
2. Однородные уравнения 1-го порядка
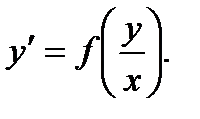
Уравнения решают с помощью замены
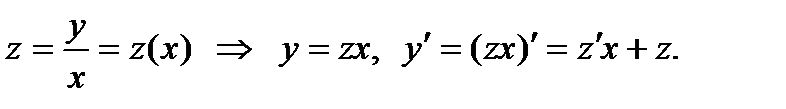
После подстановки z и 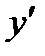 в исходное уравнение получается уравнение с разделяющимися переменными (см. п. 1).
в исходное уравнение получается уравнение с разделяющимися переменными (см. п. 1).
2.82. Решить уравнения:
1) 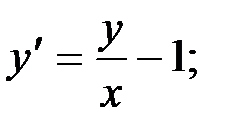 2)
2) 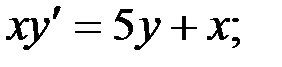 3)
3) 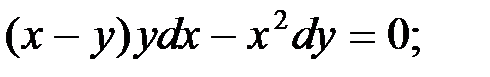
4) 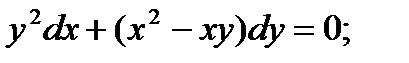 5)
5) 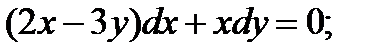
6) 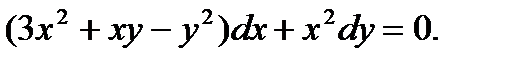
3. Линейные уравнения 1-го порядка
у ' + p (x)× y = f (x),
где p (x), f (x) – непрерывные функции.
Пример 2.12. Решить уравнение у ' + xy = x.
Решение.
Пусть 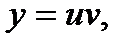 тогда
тогда 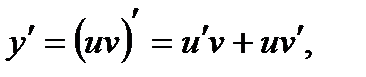 и уравнение принимает вид
и уравнение принимает вид 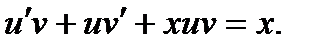
Группируя первое и третье слагаемые, получаем
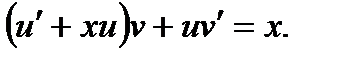
Равенство будет верным, если 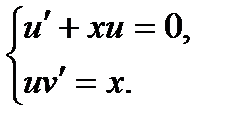
Найдем частное решение первого уравнения системы:
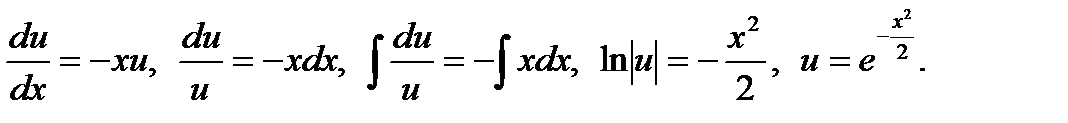
Подставим полученное решение во второе уравнение системы и найдем его общее решение:
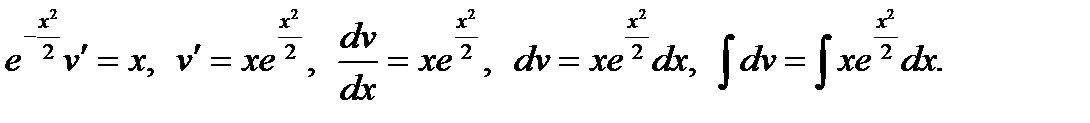
C помощью замены 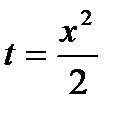 получаем общее решение:
получаем общее решение: 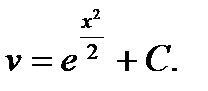
Подставляя найденные решения 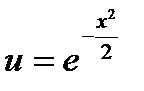 и
и 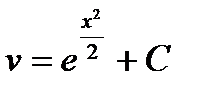 в равенство
в равенство 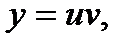 получаем решение исходного уравнения:
получаем решение исходного уравнения:
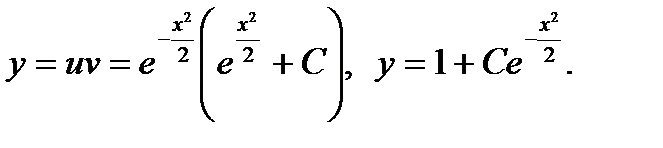
Ответ: 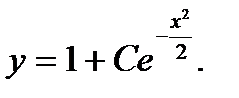
Задача Коши для уравнения 1-го порядка имеет вид
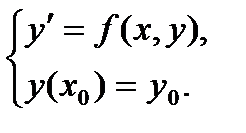
Пример 2. 13.
Решить задачу Коши 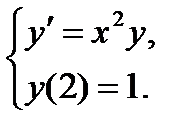
Решение.
Найдем общее решение уравнения 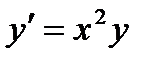 :
:
dy / dx = х 2 у |× dx/у, у ≠ 0,
dy / у = x 2 dx,
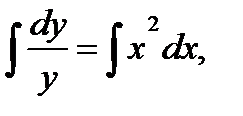
ln| y | = х 3 /3 + С.
Подставим в это решение х = 2 и у = 1 (см. условие у (2) = 1):
ln|1| = 23 /3 + С,
0 = 8/3 + С Þ С = – 8/3.
Подставляя это значение в общее решение, получаем
Ответ: ln|y| = (х3 – 8)/3.
2.83. Решить уравнение или задачу Коши:
1) 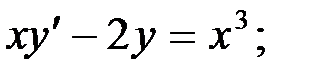 2)
2) 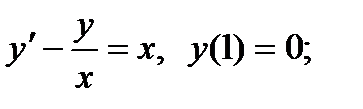
3) 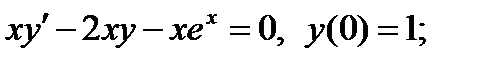 4)
4) 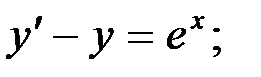
5) 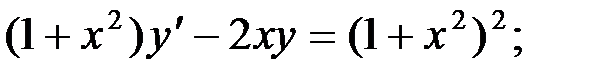 6)
6) 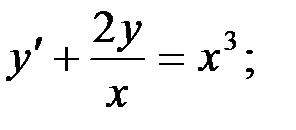
7) 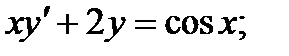 8)
8) 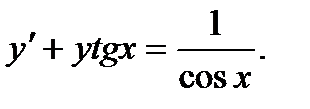
4. Линейные однородные уравнения 2-го порядка
 2015-05-12
2015-05-12 357
357








