Пример 1. Вычислите предел 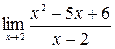 .
.
Решение.
Шаг 1. Подставим 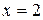 в дробь:
в дробь: 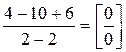 . В данном случае получена так называемая неопределенность
. В данном случае получена так называемая неопределенность 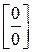 . Применим правило 1.
. Применим правило 1.
Шаг 2. Разложим числитель и знаменатель на множители. Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение: 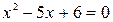 . Находим дискриминант:
. Находим дискриминант: 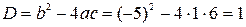 . По формуле
. По формуле 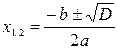 находим корни уравнения:
находим корни уравнения: 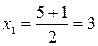 ,
, 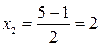 . Таким образом
. Таким образом 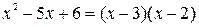 .
.
Числитель на множители разложен. Знаменатель 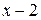 уже является простейшим множителем, и упростить его никак нельзя.
уже является простейшим множителем, и упростить его никак нельзя.
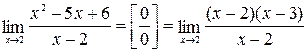 .
.
Шаг 3. Сокращаем дробь на 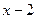 :
:
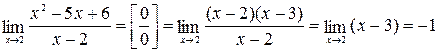 .
.
Ответ: 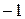 .
.
Пример 2. Вычислите предел 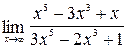 .
.
Решение.
Шаг 1. Подставим 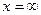 в дробь. В данном случае получена так называемая неопределенность
в дробь. В данном случае получена так называемая неопределенность 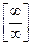 . Применим правило 2. Наивысшая степень многочленов числителя и знаменателя равна 5.
. Применим правило 2. Наивысшая степень многочленов числителя и знаменателя равна 5.
Шаг 2. Разделим числитель и знаменатель дроби на 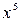 :
: 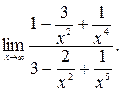
Шаг 3. Подставим 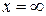 в полученное выражение и учитывая, что
в полученное выражение и учитывая, что 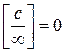 , получим:
, получим: 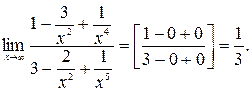
Ответ: 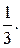
Пример 3. Вычислите предел 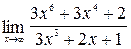 .
.
Решение. Наивысшая степень многочленов числителя и знаменателя равна 6. Делим на 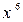 , получим:
, получим: 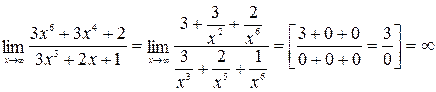 .
.
Ответ: 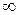 .
.
 2015-05-10
2015-05-10 405
405








