Для вычисление определенного интеграла используют формулу Ньютона-Лейбница
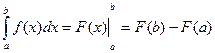
Соответствующие формулы примут вид
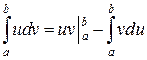 (1)
(1)
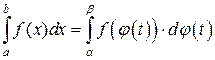 , где
, где 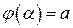 ,
, 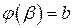 (2)
(2)
Решение типовых заданий.
Задание 1. Вычислить 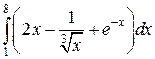 .
.
Решение:
Используя последовательно свойства (1), (2), получим
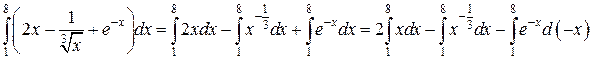 .
.
По таблице интегралов найдем первообразные для подынтегральных функций и применим формулу Ньютона-Лейбница:
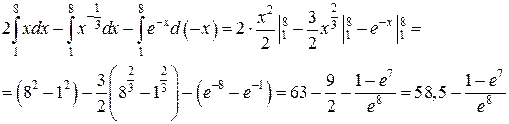
Задание 2. Вычислить 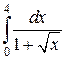 .
.
Решение:
Положим 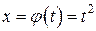 . Тогда при
. Тогда при 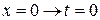 , при
, при 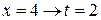 ,
, 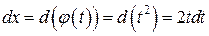 .
.
По формуле замены переменной:
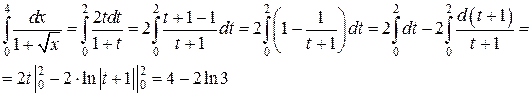
Задание 3.
Вычислить 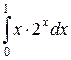 .
.
Решение:
Применим формулу (1) интегрирования по частям:
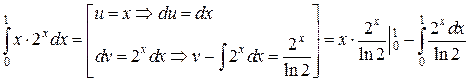 .
.
По формуле Ньютона-Лейбница имеет
 2015-05-10
2015-05-10 226
226








