2015-05-10
242
Задание 1. Найти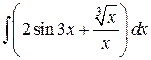 
.
Решение:
Шаг 1. Воспользуемся последовательно свойствами 4) и 3):
.
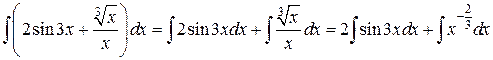Шаг 2. Так как в первом из полученных интегралов аргумент подынтегральной функции не равен аргументу, стоящему под знаком дифференциала: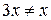 
, то преобразуем подынтегральное выражение так, чтобы они оказались равны.
.
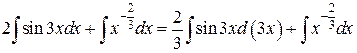Шаг 3. С помощью таблицы интегралов определим вид первообразных функций: 1)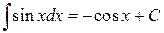 
2) 
.
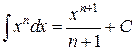
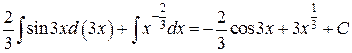Шаг 4. Выполним проверку:
.
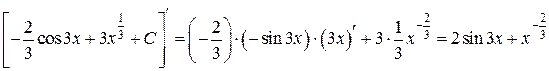Получена подынтегральная функция исходного интеграла, следовательно неопределенный интеграл найден верно.
