| И 8.2 | Определение 1. Функция, удовлетворяющая условию 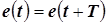 , где , где 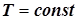 , называется периодической функцией. Определение 2. Наименьшее из всех возможных значений , называется периодической функцией. Определение 2. Наименьшее из всех возможных значений 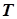 называется периодом функции называется периодом функции 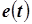 . . |
Периодическую функцию (ограниченную по величине), которая имеет конечное число экстремумов и разрывов первого рода на протяжении периода, можно разложить в тригонометрический ряд Фурье
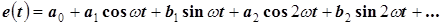 .
.
Коэффициенты этого ряда определяются по известным формулам
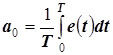 ,
,
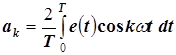 ,
,
 ,
, 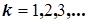 ,
,
где 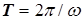 .
.
| И 8.3 | В технических дисциплинах ряд Фурье используется в следующей форме 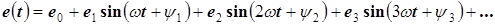 , где , где 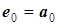 , , 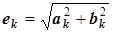 , , 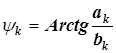 , , 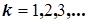 . Здесь . Здесь 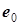 - постоянная составляющая ЭДС - постоянная составляющая ЭДС 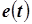 , равная среднему значению функции , равная среднему значению функции 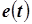 за период; составляющая за период; составляющая 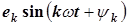 называется называется 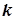 - й гармоникой ЭДС; - й гармоникой ЭДС; 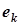 - амплитуда; - амплитуда; 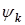 - начальная фаза - начальная фаза 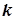 - й гармоники. - й гармоники. |
Первая гармоника (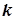 =1) называется также основной гармоникой, ее частота равна частоте периодической несинусоидальной ЭДС. Остальные гармоники называются высшими гармониками.
=1) называется также основной гармоникой, ее частота равна частоте периодической несинусоидальной ЭДС. Остальные гармоники называются высшими гармониками.
При наличии симметрии у кривой ЭДС возможны случаи, когда начальные фазы всех гармоник одинаковы (например, равны нулю) или некоторые гармоники отсутствуют.
Пример. Ряд Фурье для ЭДС, график которой показан на рис. 82, имеет вид
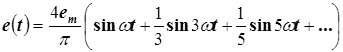 . (8.1)
. (8.1)
У этой ЭДС отсутствуют постоянная составляющая и четные гармоники, начальные фазы всех гармоник равны нулю.
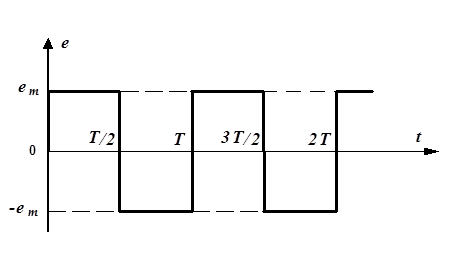
Рис. 8.2. Пример периодической несинусоидальной ЭДС
 2015-05-13
2015-05-13 1950
1950








