2015-05-13
365
Активная мощность двухполюсника по определению равна
.
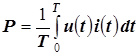Пусть напряжение и ток являются периодическими функциями времени и разложены в ряды Фурье:
,
,
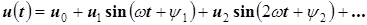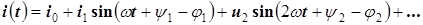где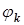 
- разность начальных фаз 
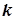-х гармоник напряжения и тока, 
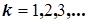. Произведение этих рядов содержит слагаемые четырех типов:
1) 
;
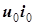2) 
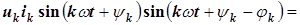
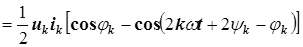; (8.4)
3) 
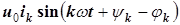или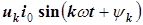 
;
4) 
,
,
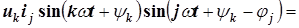
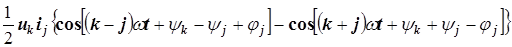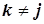здесь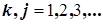 
. Так как интегралы от синусов и косинусов кратных частот за период 
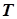равны нулю, то только слагаемые первого и второго типов вносят вклад в активную мощность:
,
= 
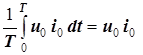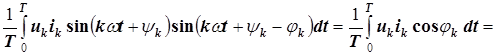
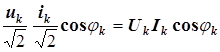, (8.5)
где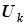 
и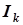 
- действующие значения 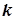- й гармоники напряжения и тока. При вычислении интеграла в формуле (8.5) использовалась формула (8.4).
С учетом результатов интегрирования получаем, что
| И 8.7 |  .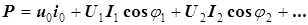
Активная мощность двухполюсника, по которому протекает периодический несинусоидальный ток, равна сумме активных мощностей, рассчитанных для отдельных гармоник, включая постоянную составляющую тока.
|
Полную мощность в цепях с несинусоидальными токами можно определять как произведение действующих значений напряжения и тока
|
|
|
.
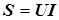Реактивную мощность в цепях с несинусоидальными токами, как правило, не определяют, так как при любом ее определении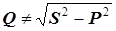 
, т.е. треугольника мощностей не существует.
