Действующее значение периодического переменного тока по определению равно
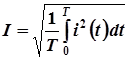 .
.
Допустим, что ток разложен в ряд Фурье:
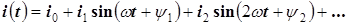 .
.
Квадрат тока содержит слагаемые четырех видов:
1) 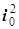 ;
;
2) 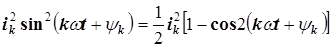 ; (8.2)
; (8.2)
3) 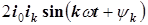 ;
;
4) 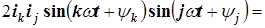
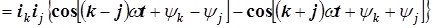 ,
, 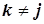 ;
;
здесь 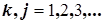 . Интегрирование синусов и косинусов кратных частот на отрезке, равном периоду тока, дает нуль. Поэтому интегралы от слагаемых третьего и четвертого типов равны нулю. Интегралы от слагаемых первого и второго типов элементарны
. Интегрирование синусов и косинусов кратных частот на отрезке, равном периоду тока, дает нуль. Поэтому интегралы от слагаемых третьего и четвертого типов равны нулю. Интегралы от слагаемых первого и второго типов элементарны

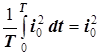 ,
,
 , (8.3)
, (8.3)
где 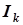 - действующее значение
- действующее значение 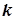 - й гармоники, в
- й гармоники, в 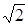 раз меньшее ее амплитуды. В процессе вычисления интеграла в формуле (8.3) было использовано преобразование, представленное формулой (8.2).
раз меньшее ее амплитуды. В процессе вычисления интеграла в формуле (8.3) было использовано преобразование, представленное формулой (8.2).
С учетом результатов интегрирования возведенного в квадрат ряда Фурье получаем, что
| И 8.5 | 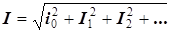 .
Действующее значение периодического несинусоидального тока равно геометрической сумме действующих значений гармоник, включая постоянную составляющую. .
Действующее значение периодического несинусоидального тока равно геометрической сумме действующих значений гармоник, включая постоянную составляющую.
|
| И 8.6 | Действующее значение периодического несинусоидального напряжения определяется аналогичным образом:
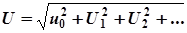 ,
где ,
где 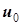 - постоянная составляющая, - постоянная составляющая, 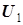 - действующее значение первой гармоники и т.д. - действующее значение первой гармоники и т.д.
|
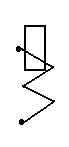
Действующие значения электрических величин измеряются приборами электромагнитной системы, которые имеют неравномерную шкалу; на лицевой панели этих приборов имеется значок, показанный на рис. 8.4,а.
|
|
|
 а)
а)
|
 б)
б)
|
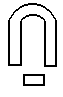
Рис. 8.4. Условные обозначения систем электроизмерительных приборов:
а) электромагнитной, б) магнитоэлектрической
Постоянные электрические величины, а также постоянные составляющие переменных электрических величин измеряются приборами магнитоэлектрической системы, которые имеют равномерную шкалу. На лицевой панели этих приборов имеется специальный значок (рис. 8.4,б).
 2015-05-13
2015-05-13 453
453








