Пример расчета. Пусть к катушке с активным сопротивлением и индуктивностью приложено напряжение , график которого показан на рис

Пусть к катушке с активным сопротивлением 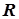и индуктивностью 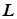приложено напряжение 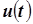, график которого показан на рис. 8.3. Требуется определить ток в катушке .

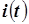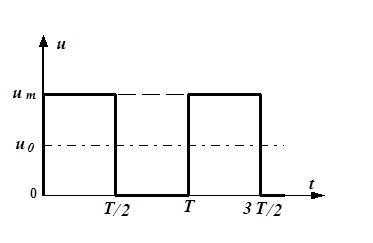
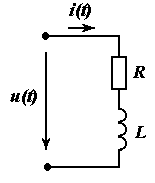
Рис. 8.3. Схема электрической цепи и график приложенного к ней

периодического несинусоидального напряжения

1. Ряд Фурье для напряжения 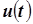можно сконструировать на основе ряда (8.1).

Постоянная составляющая напряжения

.

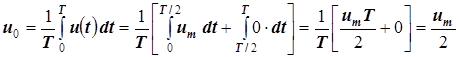Если теперь ось 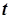поднять вверх на величину 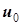(рис. 8.3), то получится график напряжения, аналогичный графику ЭДС на рис. 8.2. При этом изменению напряжения от 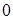до 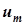(или от 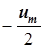до 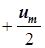после переноса оси 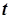) на рис. 8.3 соответствует изменение ЭДС от 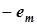до на рис. 8.2, значит, величине 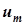на рис. 8.3 соответствует величина 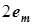на рис. 8.2. Гармоники напряжения 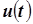получаются из гармоник ЭДС 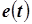заменой 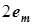на .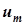

.

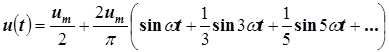2. Постоянная составляющая тока создается постоянной составляющей напряжения:

.

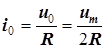Индуктивность катушки не влияет на величину постоянного тока.

3. Полное сопротивление катушки основной гармонике тока

,

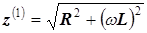основная гармоника тока отстает от основной гармоники напряжения на угол

.

Основная гармоника тока равна

,

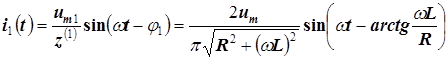где через была обозначена амплитуда основной гармоники напряжения, равная .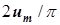

4. Вторая гармоника тока отсутствует, так как у приложенного напряжения нет второй гармоники.

Полное сопротивление катушки третьей гармонике тока

,

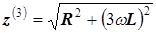разность начальных фаз третьих гармоник напряжения и тока

.

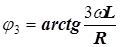Третья гармоника тока равна

.

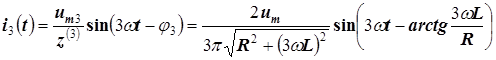По аналогии можно записать выражения для пятой и последующих гармоник тока.

5. Если пренебречь пятой и последующими гармониками тока, то искомый ток катушки равен

.

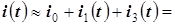
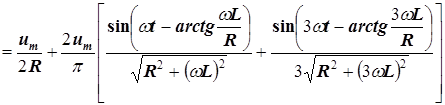Гармоники тока суммируются после того, как все они определены как функции времени.