2015-05-13
15208
Найти напряженность Е и потенциал j в центре полукольца радиусом R = 5 см, по которому равномерно распределен заряд q = 3× 
Кл.
Для определения напряженности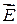 
и потенциала j в центре полукольца воспользуемся принципом суперпозиции.
Разделим полукольцо на малые элементы дуги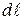 
так, чтобы заряд 
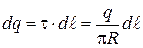каждой точки дуги можно было считать точечным.
Выберем два произвольных симметрично расположенных относительно 00/ элемента дуги (рис. 9). Напряженности электрического поля в точке 0, создаваемые выбранными элементам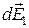и 
и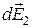 
. Согласно принципу суперпозиции 
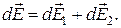Из соображений симметрии следует, что алгебраическая сумма проекций напряженностей поля выбранных элементов на ось 0 у равна нулю. Результирующее поле направлено вдоль оси 0 х:
 |
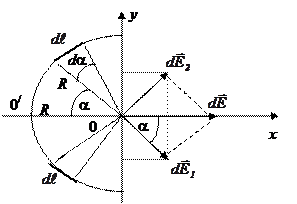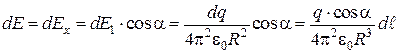. Так как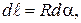 
то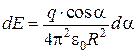 
.
Рис. 9
Положение точечного заряда dq на полукольце определяется углом a. Поэтому угол a выбираем в качестве переменной интегрирования:
;
.
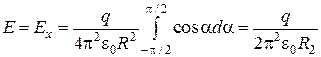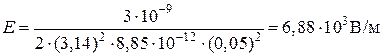Потенциал j в центре полукольца определяется алгебраической суммой потенциалов электрического поля d j элементарных зарядов (согласно принципу суперпозиции).
Учитывая, что d j точечного заряда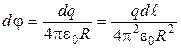 
, где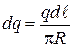 
, определяем j:
; 
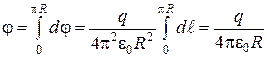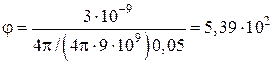В.
