Свойства функций, непрерывных на отрезке

Непрерывность элементарных функций

Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах.

Теорема. Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).

Теорема. Пусть функции u = φ (x) непрерывна в точке х ₀, а функция y = f (u) непрерывна в точке u ₀= φ (х ₀). Тогда сложная функция f (φ (x)) состоящая из непрерывных функций, непрерывна в точке x ₀.

Теорема. Если функция у = f (х) непрерывна и строго монотонна на [ а; b ] оси Ох, то обратная функция у = φ (х) также непрерывна и монотонна на соответствующем отрезке [ c; d ] оси Оу (без доказательства).

Непрерывные на отрезке функции имеют ряд важных свойств. Сформулируем их в виде теорем, не приводя доказательств.

Теорема (Вейерштрасса). Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Изображенная на рисунке 5 функция у = f (x) непрерывна на отрезке [ а; b ], принимает свое наибольшее значение М в точке x ₁, а наименьшее m - в точке х ₂. Для любого х 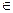[ а; b ] имеет место неравенство m ≤ f (x) ≤ М.

Рис. 5.

Следствие. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.

Теорема (Больцано - Коши). Если функция у = f (x) непрерывна на отрезке [ a; b ] и принимает на его концах неравные значения f (a) = A и f (b) = = В, то на этом отрезке она принимает и все промежуточные значения между А и В.

Геометрически теорема очевидна (см. рис. 6).

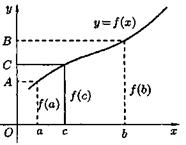
Рис. 6.

Для любого числа С, заключенного между А и В, найдется точка с внутри этого отрезка такая, что f (с) = С. Прямая у = С пересечет график функции по крайней мере в одной точке.

Следствие. Если функция у = f (x) непрерывна на отрезке [ а; b ] и на его концах принимает значения разных знаков, то внутри отрезка [ а; b ] найдется хотя бы одна точка с, в которой данная функция f (x) обращается в нуль: f (с) = 0.