В общем виде нелинейное уравнение с одним неизвестным можно представить в виде

1 2 3 4 5 6 7

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Численные методы решения нелинейных уравнений

Ый этап решения – локализация корней

Реализация 1-го этапа в MS Exсel

Ой этап - уточнение корня

Метод касательных. Реализация метода

Метод хорд. Реализация метода

Метод половинного деления. Реализация метода

Решение нелинейного уравнения с помощью надстройки «Поиск решения»

Численные методы решения нелинейных уравнений

Решение некоторых строительных задач сводится к решению достаточно сложных нелинейных уравнений, которые могут представлять собой самостоятельную задачу. Корни таких уравнений сравнительно редко удается найти точными методами. Кроме того, в некоторых случаях и коэффициенты уравнения, полученные в процессе эксперимента или как результаты предварительных расчетов, известны лишь приблизительно. Следовательно, сама задача о точном определении корней уравнения теряет смысл и важное значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности.

Нелинейными (трансцендентными) уравнениями называют уравнения, содержащие всевозможные элементарные функции (алгебраические, логарифмические, тригонометрические или показательные).

В общем виде нелинейное уравнение с одним неизвестным можно представить в виде

f (x) = 0, (1.1)

где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале a < x < b.

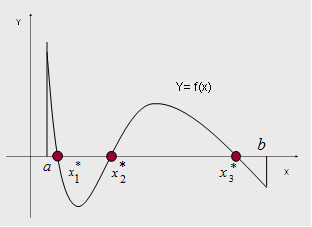Всякое значение x ^*, обращающее уравнение y=f(x) в тождество, называетсякорнемэтого уравнения, т.е. f(x^*)º 0. С геометрической точки зрения задача нахождения корней уравнения эквивалентна задаче нахождения нулей функции у=f(x) или абсцисс точек пересечения графика функции c осью Х, т.е. значений x_i, для которых выполняется условие f (x_i) = 0 (для i=1, 2,……). Исходя из специфики строительных задач, будем рассматривать только действительные корни уравнения.

Убедится в том, что на данном отрезке xÎ [a, b] (например, грубо определенном графическим способом) действительно имеется единственный корень уравнения f(x)= 0, можно аналитическим способом, в основе которого лежит известная теорема1 математического анализа.

Теорема1

Если функция у=f(x) удовлетворяет на отрезке [a, b] следующим условиям: 1. непрерывна, 2. f(a) f(b)<0, т.е. функция принимает разные знаки на концах отрезка, 3. монотонна для xÎ[a, b], т.е. производная f^’(x) сохраняет знак, то уравнение f (x) = 0 имеет единственный корень x^* на интервале [а, b].

Методы решения нелинейных уравнений делятся на 2 группы:

§ точные (прямые) и

§ итерационные (приближенные).

Точные методы позволяют записать корни уравнения в аналитическом виде, т.е. в виде некоторой формулы. Однако, многие уравнения не имеют аналитического решения.