Модальные характеристики

Модальные характеристики соответствуют свободной составляющей движения системы (2.6) или, другими словами, отражают свойства автономной системы типа (2.12)

(2.34)

Будем искать ее решение в виде экспоненты

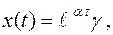(2.35)

где 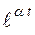- скалярная экспонента, - вектор начальных условий.

Подставляя решение (2.35) в исходное уравнение (2.34), после преобразований получим

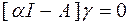. (2.36)

Система уравнений (2.36) будет иметь ненулевое решение относительно 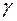, если

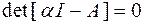. (2.37)

Уравнение (2.37) называется характеристическим и имеет n -корней , которые называются собственными значениями матрицы A. При подстановке собственных значений в (2.37) получим

.

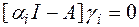где - собственные векторы,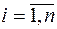

Совокупность собственных значений и собственных векторов представляет собой модальные характеристики системы.

Для (2.34) могут существовать лишь следующие экспоненциальные решения

(2.38)

которые называют модами. Полное решение системы (2.34) представляет собой линейную комбинацию мод:

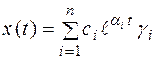. (2.39)

Для получения характеристического уравнения системы достаточно общий знаменатель передаточной матрицы (передаточной функции) приравнять нулю (2.29).