Рассмотрим метод исключения. Дана система линейных дифференциальных уравнений:
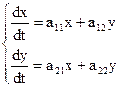 . (1)
. (1)
Исключим у из данных уравнений. Дифференцируем по t первое уравнение системы (1), при этом получим 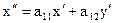 . Подставив в это равенство у/ из второго уравнения системы, будем иметь
. Подставив в это равенство у/ из второго уравнения системы, будем иметь
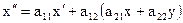 . (2)
. (2)
Переписав первое уравнение системы в виде
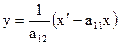 (3)
(3)
и подставив это выражение в (2), получим уравнение
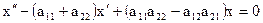 ,
,
которое является ЛОДУ второго порядка с постоянными коэффициентами. Решая его, найдем функцию 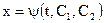 . Вторую функцию у системы (1) можно определить по формуле (3).
. Вторую функцию у системы (1) можно определить по формуле (3).
Схема решения:
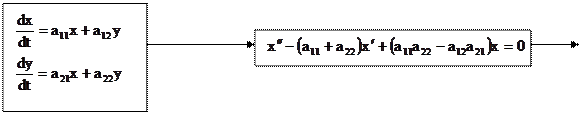 | |||
 |
Пример 1. Найти общее решение системы (методом исключения)
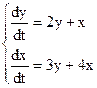 .
.
Решение. Дифференцируя первое уравнение системы, будем иметь
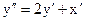
Подставив сюда х/ из второго уравнения системы, получим
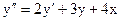 .
.
Подставим х из первого уравнения, тогда
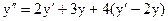 .
.
Приведем в последнем равенстве подобные члены:
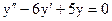 .
.
Получим ЛОДУ второго порядка. Его характеристическое уравнение 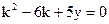 имеет два различных вещественных корня:
имеет два различных вещественных корня: 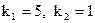 . Следовательно, решением этого дифференциального уравнения будет:
. Следовательно, решением этого дифференциального уравнения будет:
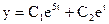 , тогда
, тогда 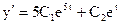 .
.
Находим вторую функцию. Из первого уравнения имеем:
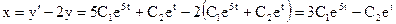 .
.
Ответ: 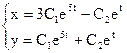 .
.
Пример. Решить систему
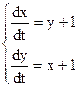 .
.
Решение. Из первого уравнения системы находим
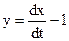 . Тогда
. Тогда 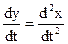 . (*)
. (*)
Подставим это выражение во второе уравнение системы:
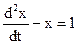 . (**)
. (**)
Получили линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его общее решение: 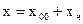 , причем
, причем 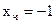 , что легко проверяется подстановкой
, что легко проверяется подстановкой 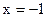 в (**). Найдем корни характеристического уравнения:
в (**). Найдем корни характеристического уравнения: 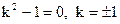 . Следовательно,
. Следовательно, 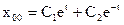 . Таким образом:
. Таким образом:
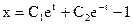 .
.
Дифференцируя это равенство и подставляя производную 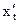 в (**), получим
в (**), получим
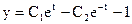 .
.
Общее решение системы:
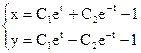 .
.
 2015-05-13
2015-05-13 2219
2219
