2015-05-13
665
 |
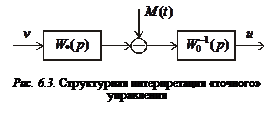
Это условие также предполагает исследование свойств объекта. Изобразим структурную схему, соответствующую выражению для «точного» управляющего воздействия (6.9). Как видим из рис. 6.3, «точный» регулятор включает в себя желаемую передаточную функцию системы и обратную модель объекта. Поскольку
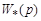всегда имеет полюса с отрицательной вещественной частью, то устойчивость «точного» регулятора определяется устойчивостью обратной модели объекта.
Отсюда следует второе условие разрешимости: задача синтеза будет иметь решение, если обратная модель объекта (6.3)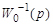 
устойчива, что соответствует требованию
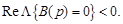(6.11)
для разрешимости задачи синтеза необходимо, чтобы все «нули» передаточной функции объекта (корни полинома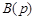 
) располагались в левой полуплоскости плоскости корней.
Пример 6.1
 |
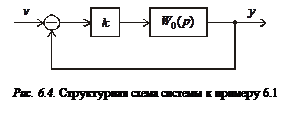Рассмотрим проявление этого условия для системы, структурная схема которой приведена на рис. 6.4. Здесь k – коэффициент усиления регулятора;
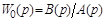– передаточная функция объекта управления.
Запишем характеристическое уравнение системы
.
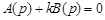Для уменьшения статической ошибки будем увеличивать коэффициент усиления регулятора. В пределе при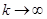 
получим вырожденную систему, характеристическое уравнение которой принимает вид
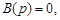
и ее устойчивость определяют «нули» передаточной функции
объекта.
Таким образом, (6.11) является необходимым условием устойчивости вырожденной системы и одновременно условием разрешимости задачи синтеза. Понятно, что для устойчивости замкнутой системы нужно анализировать все корни исходного характеристического уравнения.
