Пусть С – произвольная постоянная, 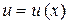 и
и 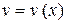 – дифференцируемые функции на интервале
– дифференцируемые функции на интервале 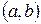 , тогда:
, тогда:
1. 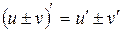 ; 3.
; 3. 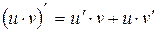 ;
;
2. 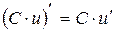 ; 4.
; 4. 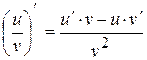 ,
, 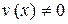 .
.
Пусть сложная функция 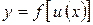 определена на области D.
определена на области D.
Если функция 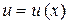 имеет производную
имеет производную 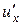 в точке
в точке 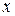 Î D, а функция
Î D, а функция 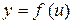 имеет производную
имеет производную 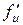 в соответствующей точке
в соответствующей точке 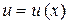 , то сложная функция
, то сложная функция 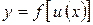 имеет производную
имеет производную 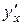 в точке
в точке 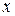 , которая находится по формуле:
, которая находится по формуле:
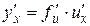 .
.
Таблица производных основных элементарных функций
1. 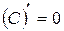 , C = const;
, C = const;
2. 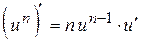 ;
;
3. 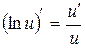 ;
;
4. 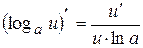 ;
;
5. 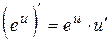 ;
;
6. 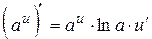 ;
;
7. 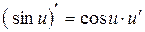 ;
;
8. 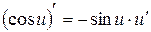 ;
;
9. 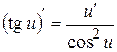 ;
;
10. 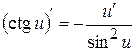 ;
;
11. 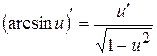 ;
;
12. 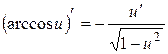 ;
;
13. 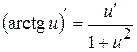 ;
;
14. 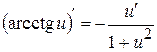 .
.
 2015-05-13
2015-05-13 240
240








