Пусть функция 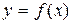 непрерывна на отрезке
непрерывна на отрезке 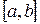 . Тогда она достигает своих наибольшего и наименьшего значений. Эти значения функция может принимать либо во внутренней точке
. Тогда она достигает своих наибольшего и наименьшего значений. Эти значения функция может принимать либо во внутренней точке 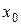 отрезка
отрезка 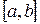 , либо на границах отрезка, т. е. при
, либо на границах отрезка, т. е. при 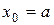 или
или 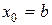 .
.
Получаем следующее правило нахождения наибольшего и наименьшего значений на отрезке 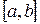 :
:
1. найти критические точки функции на интервале 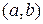 ;
;
2. вычислить значения функции в найденных критических точках и на концах отрезка, т. е. в точках 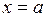 и
и 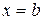 ;
;
3. среди вычисленных значений функции выбрать наибольшее и наименьшее значения функция на отрезке 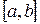 .
.
 2015-05-13
2015-05-13 317
317







