ВЫСШАЯ МАТЕМАТИКА
ДЛЯ ЭКОНОМИСТОВ
Часть I
Линейная алгебра
и
Аналитическая геометрия
Курс лекций
Лекция 1
МАТРИЦЫ
Общие сведения о матрицах
Матрицей А размерности т 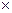 п называется прямоугольная таблица чисел:
п называется прямоугольная таблица чисел:
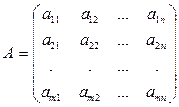 ,
,
где т - число строк матрицы, п - число столбцов матрицы. Матрицу можно записывать в виде: 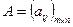 или
или 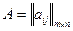 , где aij - элементы матрицы; первый индекс i указывает номер строки,
, где aij - элементы матрицы; первый индекс i указывает номер строки, 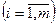 ;второй индекс j – номер столбца,
;второй индекс j – номер столбца,
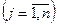 .
.
Например, 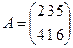 - матрица размерности 2х3;
- матрица размерности 2х3; 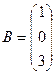 - матрица-столбец;
- матрица-столбец;
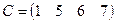 - матрица-строка.
- матрица-строка.
Матрица называется квадратной, если т = п, число п называют ее порядком.
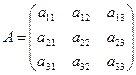 - квадратная матрица третьего порядка.
- квадратная матрица третьего порядка.
Элементы aij 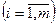 составляют главную диагональ матрицы, а элементы a1n, a2n-1,…, an1 - вспомогательную, побочную диагональ матрицы.
составляют главную диагональ матрицы, а элементы a1n, a2n-1,…, an1 - вспомогательную, побочную диагональ матрицы.
Если все aij = 0 (i 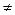 j), заисключением элементов, стоящих на главной диагонали аii, то матрицу называют диагональной, например:
j), заисключением элементов, стоящих на главной диагонали аii, то матрицу называют диагональной, например:
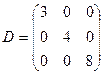
Диагональная матрица называется единичной, если все aii = 1, обозначают:
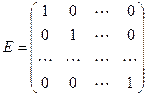 .
.
Если все aij = 0, то матрица называется нулевой, обозначают 0.
Нулевая и единичная матрицы выполняют в матричном исчислении такую же роль, как 0 и 1 в теории действительных чисел.
Две матрицы А и В называются равными, если они одной и той же размерности и их соответствующие элементы равны между собой.
А=В, если aij= bij 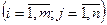 .
.
 2015-05-13
2015-05-13 653
653







