Постановка задачи. Даны точка М0(х0 ,у0 ,z0 ) и вектор 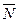 (A,B, С). Написать уравнение плоскости, проходящей через точку Мо, перпендикулярно вектору
(A,B, С). Написать уравнение плоскости, проходящей через точку Мо, перпендикулярно вектору 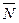 .
.
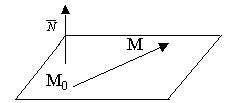
М(х, у, z) - текущая точка плоскости. Точка М принадлежит искомой плоскости тогда и только тогда, когда вектор 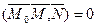 то есть, когда скалярное произведение векторов
то есть, когда скалярное произведение векторов
или в координатной форме
А(x-y0)+B(y-y0)+C(z-z0)=0.
Полученное уравнение является уравнением плоскости, проходящей через точку М0(х0 ,у0 ,z0 ) перпендикулярно вектору 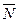 (A,B,C).
(A,B,C).
Вектор 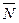 называется нормальным вектором плоскости. Если в последнем уравнении приведем подобные члены, то получим общее уравнение плоскости:
называется нормальным вектором плоскости. Если в последнем уравнении приведем подобные члены, то получим общее уравнение плоскости:
Ax+By+Cz+D=0.
Уравнение плоскости в отрезках: 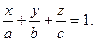
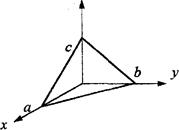
Используя условие компланарности трех векторов, можно записать уравнение плоскости, проходящей через точку M0 и параллельную векторам 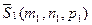 и
и 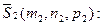
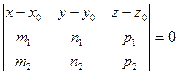
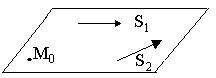
Уравнение плоскости, проходящей через три точки, имеет вид
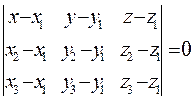
Пример 25. Найти уравнение плоскости P1, проходящей через три точки M1(1,0,4); М2(-2,1,3); М3(0,7,1) и уравнение плоскости Р2, проходящей через точку Мз, причем 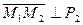
 2015-05-13
2015-05-13 344
344








