Расстояние между прямыми в пространстве

Рассмотрим две прямые l ₁ и l₂, возможны три различных случая расположения этих прямых

1) прямые пересекаются, 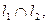следовательно, они лежат в одной плоскости Уравнения прямых

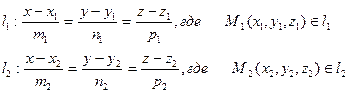
Векторы 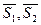и 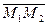, - компланарны, тогдаих смешанное произведени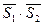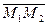е · , где 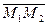=(x₂-x₁; y₂-y₁; z₂-z₁)и расстояние между прямыми d=0.

2) Прямые параллельны, 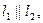тогда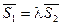

Расстояние между прямыми d можно найти, используя определение векторного произведения.

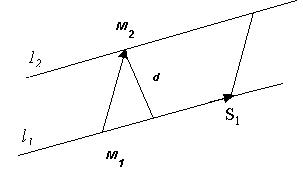
Модуль векторного произведения 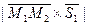- это площадь параллелограмма, тогда высота d параллелограмма равна

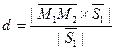
3) Прямые скрещивающиеся, они не лежат в одной плоскости, тогда искомое расстояние d определяется длиной общего перпендикуляра к этим прямым, то есть это расстояние между параллельными плоскостями, проходящими через прямые l ₁ и l₂.

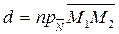
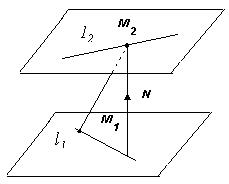
Очевидно, что нормальный вектор к плоскостям есть 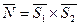. Тогда скалярное произведение:

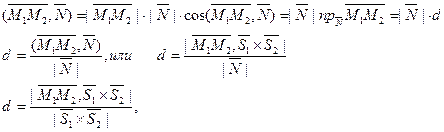
где в числителе стоит модуль смешанного произведения, или объем параллелепипеда, построенного на векторах 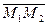, 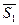и 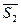, в знаменателе - модуль векторного произведения, то есть площадь параллелограмма, построенного на векторах 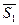и 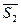. Расстояние d совпадает с высотой данного параллелепипеда.