Проверим, что заданные плоскости не параллельны, то есть их нормальные векторы неколлинеарны.
Действительно, 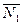 (2, -1, 1) и
(2, -1, 1) и 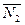 (3, 1, -1) - неколлинеарные векторы (их координаты не пропорциональны)
(3, 1, -1) - неколлинеарные векторы (их координаты не пропорциональны)
Прямая l, как линия пересечения р1 и Р2 будет перпендикулярна 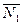 и
и 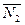 , поэтому направляющий вектор
, поэтому направляющий вектор 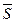 прямой l равен:
прямой l равен:
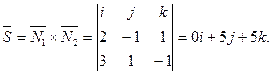
Итак, 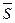 (0,5,5) Из общего уравнения прямой
(0,5,5) Из общего уравнения прямой 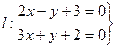
найдем любую точку, принадлежащую данной прямой Пусть z = 0, тогда, решая систему
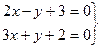
находим х=-1; y= 1 Итак, точка М(-1, 1, 0) принадлежит прямой l. Каноническое уравнение прямой имеет вид
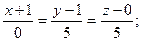
параметрические уравнения заданной прямой имеют вид
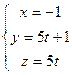
 2015-05-13
2015-05-13 419
419








