Прямая в пространстве

Прямую в пространстве можно задать как линию пересечения двух плоскостей:

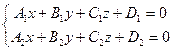
Пусть даны вектор 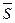(т,п, р)и точка М₀(х₀ , у₀ ,z₀). Напишем уравнение прямой l, проходящей через точку М₀ параллельно вектору .

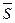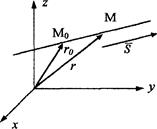
Возьмем на прямой l произвольную (текущую) точку М(х, у, z). Вектор 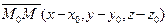коллинеарен вектору 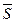(m, n,p), следовательно: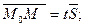

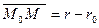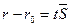так как , то или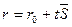

Итак, уравнение 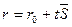называется векторным уравнением прямой в пространстве.

Вектор 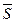(m, n, р) называется направляющим вектором прямой в пространстве.

Запишем последнее уравнение в координатной форме; так как r (х, у, z); r_o = (х₀, у₀, z₀), то

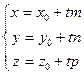
Эти уравнения называются параметрическими уравнениями прямой.

Если исключить параметр t в последних уравнениях, то получим каноническое уравнение прямой.

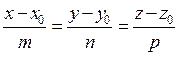
Пример 25. Найти каноническое и параметрическое уравнения прямой, заданной как пересечение двух плоскостей р₁: 2x-y+z+3=0 и Р₂: 3x+y-z+2=0