2015-05-13
655
Множество точек плоскости, координаты которых удовлетворяют уравнению Ax2+Bxy+Cy2+Dx+Ey+F=O, называется кривой второго порядка, причем хотя бы один из коэффициентов А, В, С отличен от нуля
Если А = В = С = 0, то получим уравнение первого порядка, которое определяет прямую на плоскости
Если данному уравнению не удовлетворяют координаты ни одной точки плоскости, то имеем так называемую мнимую кривую, например, x2+ у2 = -1 есть уравнение мнимой окружности.
В общем случае может оказаться, что уравнение определяет вырожденную кривую - либо пустое множество, либо точку, либо прямую, либо пару прямых (приведите примеры).
В дальнейшем рассмотрим только невырожденные кривые. Можно показать, что для таких кривых существует прямоугольная система координат, в которой уравнение этой кривой имеет один из следующих видов.
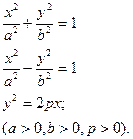
Эти уравнения называются каноническими уравнениями соответственно эллипса, гиперболы и параболы.
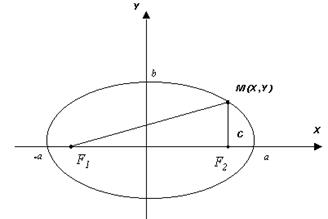
7.1 Эллипсом называется множество точек на плоскости, сумма расстояний от которых до двух данных есть величина постоянная.
|
|
|
Пусть М(х,у) - произвольная (текущая) точка кривой, F1 и F2 -заданные точки. По условию:
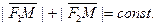
Пусть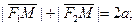 
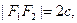тогда F1(-c;0); F2(c,0)
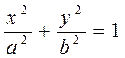каноническое уравнение эллипса
Параметры а и b называются полуосями (большой и малой) эллипса, начало координат - центром кривой. Точки f1 (-с, 0) и F2 (с, 0) называются фокусами эллипса, где с2 = а2 -b2.
Число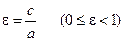 
или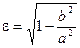 
называется эксцентриситетам эллипса, оно характеризует «сплюснутость» кривой.
В частности, при ε =0, (a =b), имеем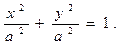 
или x2+y2=a2 - каноническое уравнение окружности радиуса а с центром в начале координат (фокусы F1 и F2 совпадают с центром).
7.2 Гиперболой называется множество точек, абсолютное значение разности расстояний от которых до двух данных точек есть величина постоянная (отличная от нуля).
По условию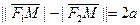 
Каноническое уравнение гиперболы: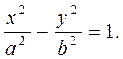 
где а и b называются полуосями гиперболы, точки (а, 0) и (-а, 0) - ее вершинами, оси симметрии ОХ и OY - соответственно действительной и мнимой осями, точки F1 (-с, 0) и F2 (с, 0) - фокусами гиперболы.
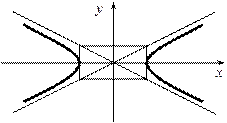Число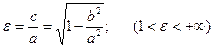 
называется эксцентриситетом гиперболы.
| |||
| |||
Прямые (диагонали прямоугольника в центре), уравнения которых
,
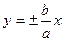являются асимптотами гиперболы.
Гиперболу, каноническое уравнение которой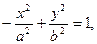 
называют сопряженной, график ее имеет следующий вид:
7.3 Параболой называется множество точек, равноотстоящих от заданной точки, называемой фокусом, и от заданной прямой, называемой директрисой.
Пусть М(х, у) - текущая точка кривой,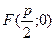 
- заданная точка, фокус;
уравнение заданной прямой (директрисы)
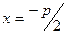
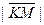- расстояние от точки М до директрисы, оно равно
|
|
|
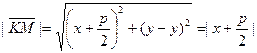
По условию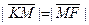 
или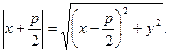 
Выполним преобразования: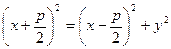 
;
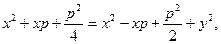
окончательно каноническое уравнение параболы:
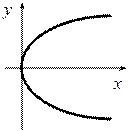y2=2xp
O
Число Р называется параметром параболы; точка O(0;0) - вершина параболы;
ось ОХ- ось симметрии параболы;
прямая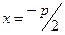 
- директриса параболы, проходит на расстоянии 
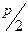от вершины параболы.
