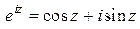 ;
; 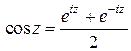 ;
; 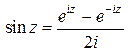 .
.
Пример 2. Представить в алгебраической форме комплексное число 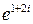 .
.
Решение. По формуле Эйлера
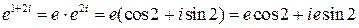 .☻
.☻
Функции 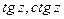 определяются равенствами
определяются равенствами 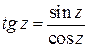 ;
; 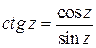 .
.
Для тригонометрических функций остаются в силе все формулы тригонометрии.
3. Гиперболические функции 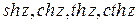 определяются равенствами
определяются равенствами
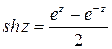 ;
; 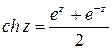 ;
; 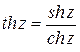 ;
; 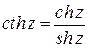 .
.
Связь между тригонометрическими и гиперболическими функциями
Задача 1. Используя формулы Эйлера, доказать соотношения
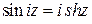 ;
; 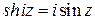 ;
;
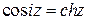 ;
; 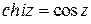 ;
;
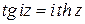 ;
; 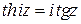 ;
;
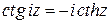 ;
; 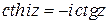 ,
,
а также следующие формулы
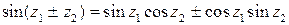 ;
;
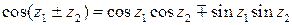 ;
;
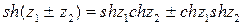 ;
;
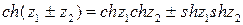 ;
;
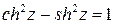 ;
;
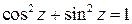 .
.
Пример 3. Выделить действительную и мнимую части функции 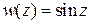 .
.
Решение. Полагаем 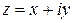 , тогда
, тогда
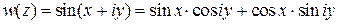 .
.
В силу соотношений задачи 1 имеем 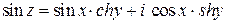 , то есть
, то есть 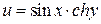 ,
, 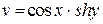 . ☻
. ☻
4. Логарифмическая функция 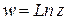 ,
, 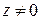 , определяется как функция, обратная показательной. Если
, определяется как функция, обратная показательной. Если 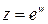 ,
, 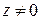 , то
, то 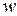 называется логарифмом числа
называется логарифмом числа 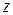 . Полагая
. Полагая 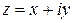 ,
, 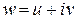 , получим
, получим 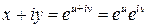 или
или 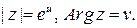
Значит,
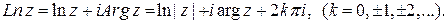
Эта функция является многозначной. Главным значением функции 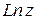 называется то значение, которое соответствует главному значению аргумента числа
называется то значение, которое соответствует главному значению аргумента числа 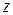 :
:
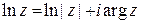 .
.
Для логарифмической функции справедливы следующие соотношения:
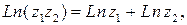
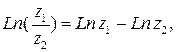
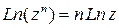 .
.
В качестве упражнения рекомендуем доказать эти три соотношения.
Пример 4. Представить в алгебраической форме комплексное число 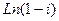 .
.
Решение. 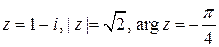 (см. пример 10, §1). Таким образом,
(см. пример 10, §1). Таким образом,
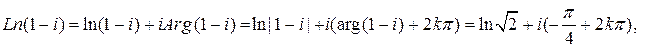
 ☻
☻
5. Общая степенная функция 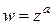 , где
, где 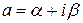 – любое комплексное число, определяется равенством
– любое комплексное число, определяется равенством 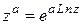 .
.
В силу многозначности логарифма функция 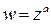 многозначна. Главное значение функции
многозначна. Главное значение функции 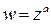 соответствует главному значению
соответствует главному значению 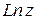 :
: 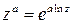 .
.
6. Общая показательная функция 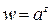 , где
, где 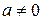 – любое комплексное число, определяется равенством
– любое комплексное число, определяется равенством
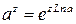 .
.
Главное значение этой функции 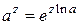 .
.
Пример 5. Найти 1) 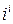 ; 2)
; 2) 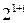 ; 3)
; 3) 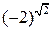 .
.
Решение. Согласно формуле п.6 1) 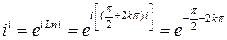 .
.
2) 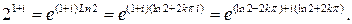
3) Решить самостоятельно. Ответ: 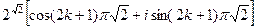 . ☻
. ☻
7. Обратные тригонометрические функции 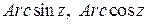 определяются как функции, обратные соответственно к синусу и косинусу:
определяются как функции, обратные соответственно к синусу и косинусу:
если 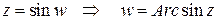 , если
, если 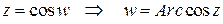 .
.
Аналогично определяются функции 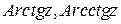 , а также обратные гиперболические функции. Все эти функции являются многозначными и выражаются через логарифмические:
, а также обратные гиперболические функции. Все эти функции являются многозначными и выражаются через логарифмические:
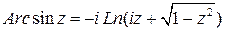 ;
; 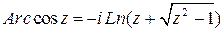 ;
;
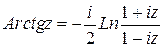 ;
; 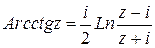 ;
;
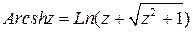 ;
; 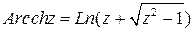 .
.
Покажем справедливость первого соотношения. Если 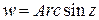 , то
, то 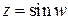 . На основании формул Эйлера
. На основании формул Эйлера 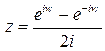 , откуда
, откуда 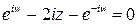 или
или 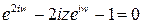 . Решая это квадратное относительно
. Решая это квадратное относительно 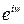 уравнение, получим
уравнение, получим 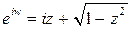 . (Здесь символом
. (Здесь символом 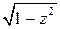 обозначены оба значения корня). Значит,
обозначены оба значения корня). Значит, 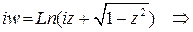
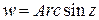 =
= 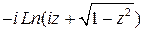 .
.
Оставшиеся соотношения рекомендуем показать в качестве упражнения.
Пример 6. Найти все значения 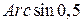 .
.
Решение. 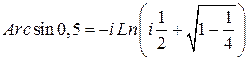
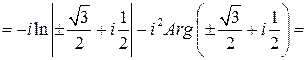
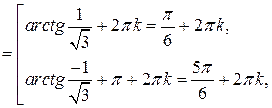
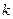 - целое. ☻
- целое. ☻
 2015-05-13
2015-05-13 2524
2524








