1. Найти пределы 1) 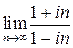 ; 2)
; 2) 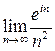 .
.
2. Исследовать сходимость рядов:
1) 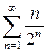 ; 2
; 2 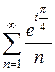 ; 3)
; 3) 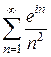 ; 4)
; 4) 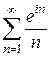 .
.
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Определение. В области 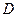 задана функция комплексной переменной
задана функция комплексной переменной 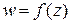 , если каждому значению
, если каждому значению 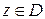 по определенному закону поставлено в соответствие одно (в случае однозначной функции) или большее число (в случае многозначной функции) значений
по определенному закону поставлено в соответствие одно (в случае однозначной функции) или большее число (в случае многозначной функции) значений 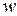 .
.
Всякая функция 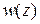 комплексной переменной
комплексной переменной 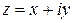 представима в виде
представима в виде
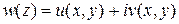 ,
,
где 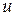 (действительная часть функции) и
(действительная часть функции) и 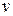 (мнимая часть) суть действительные функции действительных переменных
(мнимая часть) суть действительные функции действительных переменных 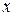 и
и 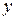 .
.
Пример 1. Найти действительную и мнимую части функции
1) 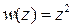 ; 2)
; 2) 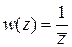 .
.
Решение. Полагая 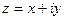 , запишем
, запишем
1) 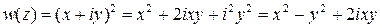 . Значит,
. Значит, 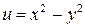 ,
, 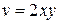 .
.
2) 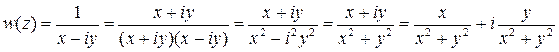 .
.
Значит, 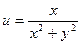 ,
, 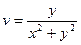 . ☻
. ☻
 2015-05-13
2015-05-13 1497
1497








