Пусть функция комплексной переменной 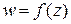 определена в области
определена в области 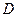 , и пусть точки
, и пусть точки 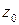 и
и 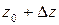 принадлежат области
принадлежат области 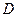 . Обозначим
. Обозначим
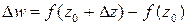 .
.
Определение. Функция 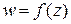 называется дифференцируемой в точке
называется дифференцируемой в точке 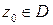 , если существует предел разностного отношения
, если существует предел разностного отношения 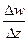 при стремлении
при стремлении 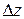 к нулю произвольным образом. Этот предел называется производной функции
к нулю произвольным образом. Этот предел называется производной функции 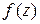 в точке
в точке 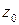 и обозначается символом
и обозначается символом 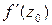 , то есть
, то есть
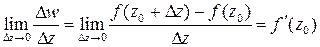 .
.
Пример 1. Убедиться, что функция 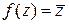 не дифференцируема ни в одной точке
не дифференцируема ни в одной точке 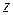 комплексной плоскости.
комплексной плоскости.
Решение. Имеем 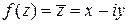 . Составим разностное отношение
. Составим разностное отношение
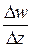
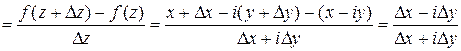 .
.
Покажем, что предел отношения 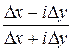 зависит от способа стремления
зависит от способа стремления 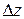 к нулю. Действительно, при стремлении
к нулю. Действительно, при стремлении 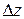 к нулю вдоль линии, параллельной действительной оси, имеем
к нулю вдоль линии, параллельной действительной оси, имеем 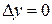 ,
, 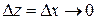 и
и 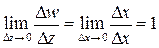 . А при стремлении
. А при стремлении 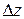 к нулю вдоль линии, параллельной мнимой оси, имеем
к нулю вдоль линии, параллельной мнимой оси, имеем 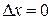 ,
, 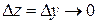 и
и 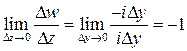 . Значит, при стремлении
. Значит, при стремлении 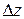 к нулю произвольным образом предел отношения
к нулю произвольным образом предел отношения 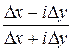 , а с ним и производная функции
, а с ним и производная функции 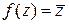 не существует ни в одной точке. ☻
не существует ни в одной точке. ☻
Требование дифференцируемости функции комплексной переменной в точке 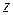 налагает определенные условия на поведение действительной и мнимой частей этой функции в окрестности точки
налагает определенные условия на поведение действительной и мнимой частей этой функции в окрестности точки 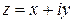 . Имеют место следующие утверждения:
. Имеют место следующие утверждения:
1. Если функция 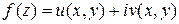 дифференцируема в точке
дифференцируема в точке 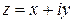 , то в точке
, то в точке 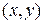 существуют частные производные функций
существуют частные производные функций 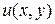 и
и 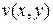 по переменным
по переменным 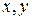 , причем выполняются соотношения (условия Коши-Римана)
, причем выполняются соотношения (условия Коши-Римана)
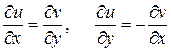 . (К.-Р.)
. (К.-Р.)
2. Если в точке 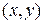 функции
функции 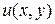 и
и 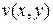 дифференцируемы, а их частные производные связаны условиями К.-Р., тофункция
дифференцируемы, а их частные производные связаны условиями К.-Р., тофункция 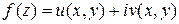 является дифференцируемой функцией комплексной переменной в точке
является дифференцируемой функцией комплексной переменной в точке 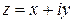 .
.
Определение. Если функция 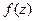 дифференцируема во всех точках области
дифференцируема во всех точках области 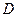 , то она называется аналитическойв области
, то она называется аналитическойв области 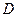 .
.
Необходимым и достаточным условием аналитичности функции 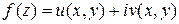 в области
в области 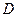 является существование в этой области непрерывных частных производных функций
является существование в этой области непрерывных частных производных функций 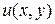 и
и 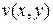 , связанных соотношениями К.-Р.
, связанных соотношениями К.-Р.
Производная аналитической функции 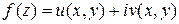 представляется одной из следующих формул:
представляется одной из следующих формул:
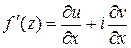 ;
; 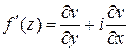 ;
; 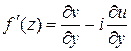 ;
; 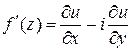 .(*)
.(*)
Известные правила дифференцирования суммы, разности, произведения, частного, степени, сложной и обратной функции остаются справедливыми и в случае комплексного аргумента.
Пример 2. Показать, что функция 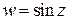 является аналитической на всей комплексной плоскости. Найти производную этой функции.
является аналитической на всей комплексной плоскости. Найти производную этой функции.
Решение. Представим заданную функцию в виде 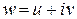 . Имеем
. Имеем
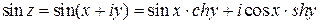 .
.
Функции 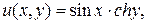
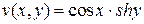 как функции действительных переменных
как функции действительных переменных 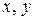 имеют непрерывные частные производные в любой точке
имеют непрерывные частные производные в любой точке 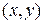 . Вычисляем
. Вычисляем 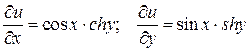 ;
; 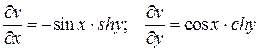 .
.
Условия К.-Р. выполняются. Следовательно, функция 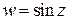 является аналитической на всей комплексной плоскости. Производную найдем, например, по первой из четырех формул (*):
является аналитической на всей комплексной плоскости. Производную найдем, например, по первой из четырех формул (*):
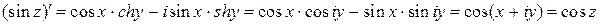 .
.
Определение. Функция 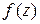 называется аналитической в точке
называется аналитической в точке 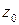 , если она дифференцируема как в самой точке
, если она дифференцируема как в самой точке 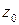 , так и в некоторой ее окрестности. Иначе, аналитичность функции
, так и в некоторой ее окрестности. Иначе, аналитичность функции 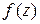 в точке
в точке 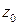 означает ее аналитичность в некоторой окрестности этой точки.
означает ее аналитичность в некоторой окрестности этой точки.
Пример 3. Может ли функция 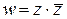 быть аналитической хотя бы в одной точке комплексной плоскости?
быть аналитической хотя бы в одной точке комплексной плоскости?
Решение. Выделим действительную и мнимую части заданной функции:
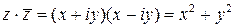 .
.
Значит, 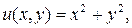
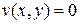 . Функции
. Функции 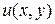 и
и 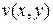 имеют непрерывные производные в любой точке
имеют непрерывные производные в любой точке 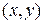 , но условия К.-Р.
, но условия К.-Р. 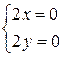 выполняются только в точке
выполняются только в точке 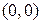 . Следовательно, функция
. Следовательно, функция 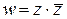 дифференцируема только в точке
дифференцируема только в точке 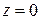 , поэтому не может быть аналитической даже в этой точке. ☻
, поэтому не может быть аналитической даже в этой точке. ☻
Точки плоскости, в которых однозначная функция 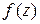 является аналитической, называют правильными точками этой функции, а точки, в которых функция
является аналитической, называют правильными точками этой функции, а точки, в которых функция 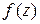 не является аналитической (в частности, точки, в которых функция не определена), – особыми точками.
не является аналитической (в частности, точки, в которых функция не определена), – особыми точками.
Определение. Функция 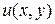 называется гармонической в области
называется гармонической в области 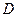 , если она всюду в области
, если она всюду в области 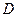 имеет непрерывные частные производные первого и второго порядков и удовлетворяет уравнению Лапласа
имеет непрерывные частные производные первого и второго порядков и удовлетворяет уравнению Лапласа 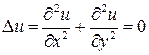 .
.
Пример 4. Показать, что функция 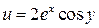 является гармонической.
является гармонической.
Решение. Находим
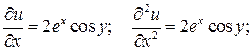
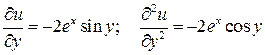
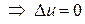 ☻
☻
Задача 1. Убедиться, что действительная и мнимая части аналитической функции являются гармоническими функциями.
Определение. Две гармонические функции, удовлетворяющие условиям Коши-Римана, называются сопряженными гармоническими функциями.
Пример 5. Даны функции 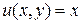 ,
, 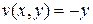 . Являются ли они сопряженными гармоническими функциями?
. Являются ли они сопряженными гармоническими функциями?
Решение. Очевидно, что функции 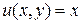 и
и 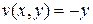 гармонические. Проверим условия К.-Р.:
гармонические. Проверим условия К.-Р.:
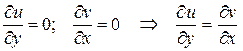
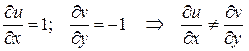 .
.
Видим, что одно из этих условий не выполнено. Значит, 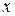 и
и 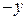 не являются сопряженными гармоническими функциями. ☻
не являются сопряженными гармоническими функциями. ☻
Пример 6. Дана функция 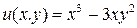 . Можно ли принять ее за действительную часть аналитической функции? Если да, то какой именно?
. Можно ли принять ее за действительную часть аналитической функции? Если да, то какой именно?
Решение. Легко проверить, что данная функция удовлетворяет уравнению Лапласа. Значит, ее можно принять за действительную часть некоторой аналитической функции 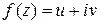 . Найдем
. Найдем 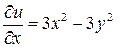 ;
; 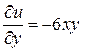 . Подставляя эти производные в условия Коши-Римана, получим
. Подставляя эти производные в условия Коши-Римана, получим 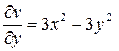 ;
; 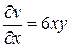 . Первое соотношение дает
. Первое соотношение дает
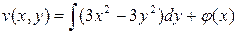
(вместо постоянной появляется произвольная функция от переменной 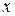 , по которой не производилось интегрирование). Значит,
, по которой не производилось интегрирование). Значит, 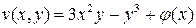 . Для определения неизвестной функции
. Для определения неизвестной функции 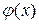 дифференцируем
дифференцируем 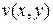 по
по 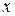 :
: 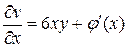 и сравниваем со вторым соотношением:
и сравниваем со вторым соотношением: 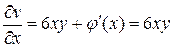 . Отсюда заключаем, что
. Отсюда заключаем, что 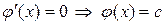 . Значит,
. Значит, 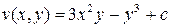 . Окончательно,
. Окончательно,
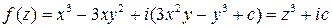 . ☻
. ☻
 2015-05-13
2015-05-13 10055
10055
