Предел функции комплексной переменной. Непрерывность

Пусть однозначная функция комплексной переменной 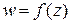определена в области .

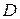Определение. Число 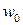называется предельным значением функции 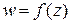вточке , , 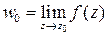если 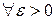можно указать такое 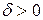, , 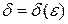что для всех точек 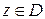, удовлетворяющих условию 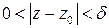, имеет место неравенство .

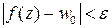Пример 1. Найти .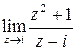

Решение. . ☻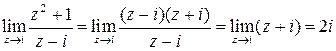

Определение. Функция 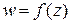непрерывна в точке 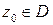, если предельное значение этой функции в точке существует и совпадает с частным значением функции 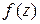в этой точке, то есть .

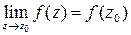Иначе: функция 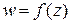непрерывнавточке 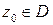, если 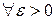можно указать такое 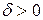, , 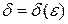что для всех точек 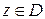, удовлетворяющих условию 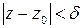, имеет место неравенство .

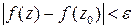Функция, непрерывнаявкаждой точке области 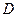, называется непрерывной в этой области. Точкой разрыва функции называется точка, в которой нарушается непрерывность.

Пример 2. Функция 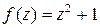непрерывна на всей комплексной плоскости; функция 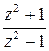имеет две точки разрыва 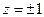; функция 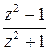терпит разрыв в точках . ☻

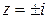Непрерывность функции 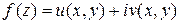равносильна непрерывности двух действительных функци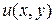й и .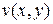

Определение. Функция 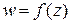равномерно непрерывна в области 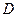, если 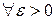можно указать такое 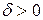, , 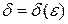что для любых двух точек 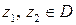, расстояние между которыми меньше 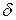: 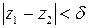, расстояние между соответствующими значениями функции меньше : .

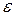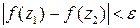Пример 3. Функция 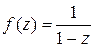непрерывна в круге 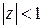и равномерно непрерывна в замкнутом круг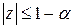е , где 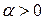, то есть в круге радиуса немного меньше единицы. ☻