При изучении раздела “Теория вычетов и ее приложения” следует прежде всего усвоить понятие интеграла от функции комплексной переменной. Вычисление интеграла от функции 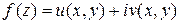 комплексной переменной
комплексной переменной 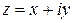 по кривой
по кривой 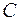 сводится к вычислению криволинейных интегралов второго рода:
сводится к вычислению криволинейных интегралов второго рода: 
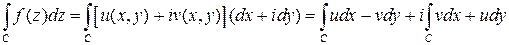 . (1)
. (1)
Основные свойства интеграла:
1. Линейность: 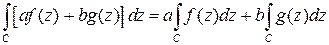 .
.
2. Аддитивность: 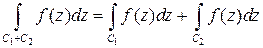 .
.
3. Изменение знака при изменении направления: 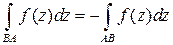 .
.
4. Оценка интеграла по модулю: 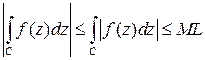 .
.
Здесь 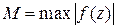 на кривой интегрирования,
на кривой интегрирования, 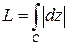 – длина этой кривой.
– длина этой кривой.
Если 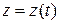 – параметрическое уравнение кривой интегрирования, а
– параметрическое уравнение кривой интегрирования, а 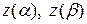 соответственно начало и конец этой кривой, то имеет место формула
соответственно начало и конец этой кривой, то имеет место формула
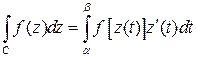 (2)
(2)
Если путь интегрирования – окружность с центром в точке 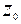 радиуса
радиуса 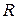 , то следует делать замену переменной вида
, то следует делать замену переменной вида 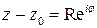
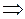
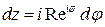 . Здесь
. Здесь 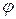 –действительная переменная интегрирования.
–действительная переменная интегрирования.
Пример 1. Вычислить интеграл 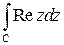 , где дуга
, где дуга 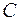 представляет собой
представляет собой
а) прямолинейный отрезок, соединяющий точку 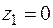 с точкой
с точкой 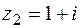 ;
;
б) ломаную 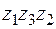 , где
, где 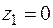 ,
, 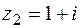 ,
, 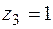 ;
;
в) параболу 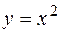 .
.
Решение. Применяя формулу (1), получим
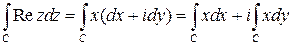 .
.
а) Уравнение прямой, соединяющей точки 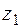 и
и 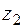 , имеет вид
, имеет вид 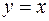
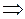
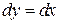 , здесь
, здесь 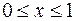 . Поэтому
. Поэтому
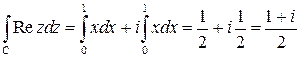 .
.
б) На отрезке 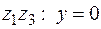
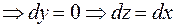 ,
, 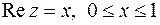 ;
;
на отрезке 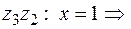
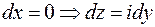 ,
, 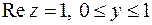 .
.
Используя свойство аддитивности, получаем
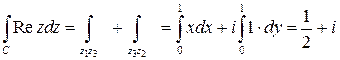 .
.
в) Для параболы 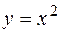 имеем
имеем 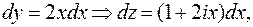
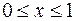 .
.
Значит, 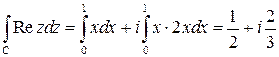 .
.
Получили три различных результата. Этот пример показывает, что интеграл от непрерывной, но не аналитической функции 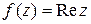 зависит от пути интегрирования.
зависит от пути интегрирования.
Ниже (§7) будет показано, что интеграл от функции 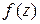 , однозначной и аналитической в односвязной области
, однозначной и аналитической в односвязной области 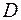 , не зависит от пути интегрирования.
, не зависит от пути интегрирования.
Задача 1. Вычислить 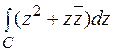 , где
, где 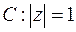 ,
, 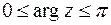 (начало интегрирования в точке
(начало интегрирования в точке 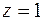 ). Ответ: -
). Ответ: - 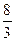 .
.
Если однозначная функция 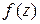 аналитична в односвязной области
аналитична в односвязной области 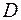 , то интеграл
, то интеграл 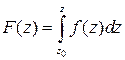 ,
, 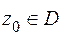 как функция верхнего предела является аналитической функцией в области
как функция верхнего предела является аналитической функцией в области 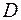 и представляет собой одну из первообразных функций
и представляет собой одну из первообразных функций 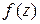 , то есть
, то есть 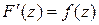 . Имеет место формула Ньютона-Лейбница:
. Имеет место формула Ньютона-Лейбница:
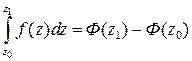 ,
,
где 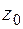 ,
, 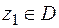 , а
, а 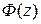 – какая-либо первообразная функции
– какая-либо первообразная функции 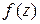 .
.
Если функции 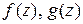 – аналитические в односвязной области
– аналитические в односвязной области 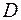 и точки
и точки 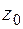 ,
, 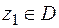 , то имеет место формула интегрирования по частям:
, то имеет место формула интегрирования по частям:
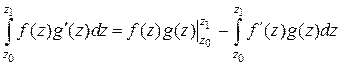 .
.
Пример 2. Вычислить интеграл 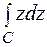 , где
, где 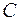 – верхняя половина эллипса
– верхняя половина эллипса 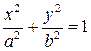 , начало пути в точке
, начало пути в точке 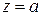 .
.
Решение. 1 способ. Параметрические уравнения эллипса 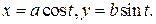 Значит,
Значит, 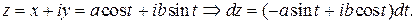 Начальной точке интегрирования соответствует значение параметра
Начальной точке интегрирования соответствует значение параметра  , для конечной точки
, для конечной точки 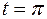 .
.
Следовательно,
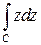 =
= 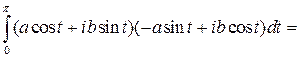
= 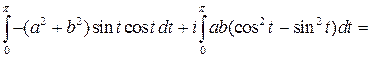
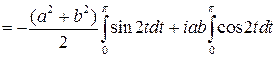
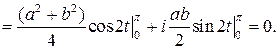
2 способ. Подынтегральная функция 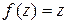 – аналитическая на всей комплексной плоскости, значит, интеграл не зависит от пути интегрирования (только от начальной и конечной точки) и можно вычислить его по формуле Ньютона-Лейбница
– аналитическая на всей комплексной плоскости, значит, интеграл не зависит от пути интегрирования (только от начальной и конечной точки) и можно вычислить его по формуле Ньютона-Лейбница
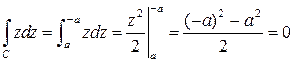 .?
.?
Пример 3. Вычислить интеграл 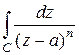 , где
, где 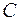 – окружность
– окружность 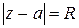 ,
, 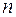 – целое положительное число (окружность обходится против часовой стрелки).
– целое положительное число (окружность обходится против часовой стрелки).
Решение. Положим 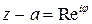
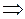
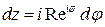 . Тогда
. Тогда
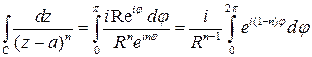 .
.
Рассмотрим сначала случай 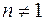 и напомним, что функция
и напомним, что функция 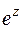 имеет период
имеет период 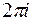 . Тогда
. Тогда 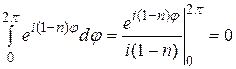 . Когда
. Когда 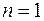 , то
, то 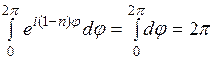 .
.
Значит, 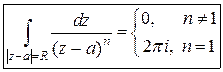 .
.
Заметим, что результат не зависит ни от радиуса 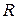 , ни от точки
, ни от точки 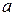 .?
.?
Пример 4. Оценить по модулю интеграл 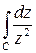 , где
, где 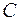 – верхняя половина окружности
– верхняя половина окружности 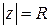 .
.
Решение. На кривой интегрирования модуль подынтегральной функции 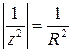 , длина этой кривой
, длина этой кривой 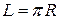 . Согласно свойству 4 имеем
. Согласно свойству 4 имеем
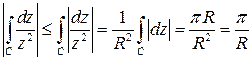 .?
.?
 2015-05-13
2015-05-13 28832
28832
