Кривизна кривой на поверхности

Пусть F – регулярная поверхность класса С² и 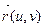- ее векторная параметризация, заданная на Q, а g - регулярная кривая класса С² на данной поверхности с внутренними уравнениями 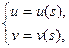, где s – натуральный параметр на кривой g, а 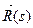= 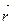(u(s), v(s)) - ее векторное уравнение.

Пусть М(u,v) - произвольная точка кривой g. Обозначим: 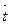- единичный касательный вектор к кривой g в точке М,

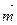- главный нормальный вектор к кривой g в точке М,

k – кривизна кривой g в точке М,

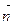- нормальный вектор к поверхности F в точке М,

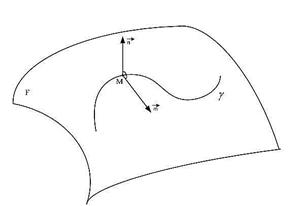
j - угол между векторам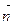и и .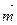

По первой формуле Френе

.

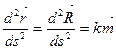Тогда, умножив предыдущее равенство скалярно на нормальный вектор 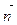, получим:

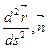() = k (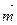, 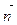) = k cos j.

С другой стороны,

II = (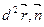), I = ds².

Отсюда получим:

k×cos j = 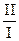= 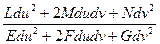. (4)

Правая часть равенства (4) зависит только от направления кривой в данной точке, так как значения коэффициентов в этой точке будут фиксированными. Кроме того, правая часть в данной точке будет постоянной для всех кривых, проходящих через эту точку и имеющих одну и ту же касательную. Это отношение называют нормальной кривизной поверхности в данной точке в данном направлении и обозначают k₀. Равенство (4) принимает вид:

k cos j = k₀. (5)

Равенство (5) называют теоремой Менье.

Если пересечь поверхность F плоскостью, проходящей через её точку М и перпендикулярно к касательной плоскости, то в сечении мы получим кривую, которая называется нормальным сечением поверхности. Так как в этом случае j = 0 или p, то кривизна нормального сечения будет равна нормальной кривизне с точностью до знака.