Пусть F – регулярная поверхность класса С2 и 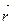 =
= 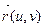 - ее векторная параметризация, заданная на Q. Пусть точка О Î F. Рассмотрим в точке О касательную плоскость p и введем прямоугольную декартовую систему координат Охуz - такую, чтобы оси Ох и Оу лежали в плоскости p, а ось Оz была направлена по нормали
- ее векторная параметризация, заданная на Q. Пусть точка О Î F. Рассмотрим в точке О касательную плоскость p и введем прямоугольную декартовую систему координат Охуz - такую, чтобы оси Ох и Оу лежали в плоскости p, а ось Оz была направлена по нормали
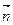 (u,v) =
(u,v) = 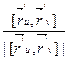 .
.
Как было доказано (см. §2 теорема 2), в этой системе координат поверхность F может быть задана явным уравнением вида
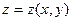 ,
,
или в параметрическом виде: 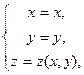
причем функция 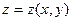 к -регулярная, к ≥ 2, и в точке О имеем:
к -регулярная, к ≥ 2, и в точке О имеем:
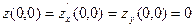 .
.
Разлагая функцию 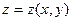 по формуле Тейлора в точке О, получим:
по формуле Тейлора в точке О, получим:
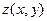 =
= 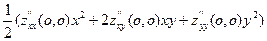 +x
+x 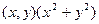 , (1)
, (1)
где 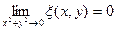 .
.
Обозначим
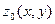 =
= 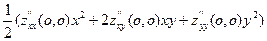 (2)
(2)
и назовем поверхность F0, заданную функцией 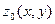 , соприкасающимся параболоидом поверхности F в точке О.
, соприкасающимся параболоидом поверхности F в точке О.
Нетрудно показать, что все первые и вторые производные функций 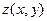 и
и 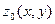 в точке (0, 0) совпадают. Поскольку коэффициенты первой и второй квадратичных форм выражаются только через первые и вторые производные рассматриваемых функций, то в точке О у поверхности F и её соприкасающегося параболоида F0 совпадают первая и вторая квадратичные формы, а значит, и все те геометрические характеристики, которые через них выражаются. В частности, у поверхности F и её соприкасающегося параболоида F0 в точке О одни и те же нормальные кривизны по одинаковым направлениям.
в точке (0, 0) совпадают. Поскольку коэффициенты первой и второй квадратичных форм выражаются только через первые и вторые производные рассматриваемых функций, то в точке О у поверхности F и её соприкасающегося параболоида F0 совпадают первая и вторая квадратичные формы, а значит, и все те геометрические характеристики, которые через них выражаются. В частности, у поверхности F и её соприкасающегося параболоида F0 в точке О одни и те же нормальные кривизны по одинаковым направлениям.
Из курса аналитической геометрии известно, что поворотом осей координат Ох и Оу в плоскости Оху уравнение соприкасающегося параболоида можно привести к каноническому виду:
Z0 = 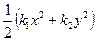 . (3)
. (3)
Определение 1. Направления в точке О, соответствующие координатным осям Ох и Оу, когда уравнение соприкасающегося параболоида имеет канонический вид (3), называются главными направлениями поверхности F в точке О.
Определение 2. Нормальные кривизны поверхности F в точке О, вычисленные в главных направлениях, называются главными нормальными кривизнами поверхности F в точке О, а нормальные сечения в этих направлениях называются главными нормальными сечениями.
Выясним геометрический смысл коэффициентов к1 и к2 в уравнении (3). Для этого вычислим нормальные кривизны соприкасающегося параболоида в точке O в направлении новых осей координат.
Ранее мы нашли коэффициенты первой и второй квадратичных форм поверхности 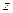 =
= 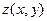 :
:
Е = 1 + 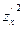 , F =
, F = 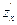 ×
× 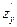 , G = 1 +
, G = 1 + 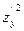 ,
,
L = 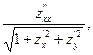 M =
M = 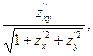 N =
N = 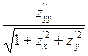 .
.
Так как
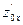 = k1x,
= k1x, 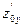 = k2y,
= k2y, 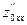 = k1,
= k1, 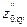 = 0,
= 0, 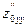 = k2,
= k2,
то находим, при условии, что х = 0 и у = 0:
I = dx2 + dy 2 (4)
и
II= k1 dx2 + k2dy2. (5)
Напомним, что в точке О первая и вторая квадратичные формы соприкасающегося параболоида и самой поверхности совпадают.
Находим нормальную кривизну соприкасающегося параболоида и поверхности в точке О в направлениях осей координат из формулы:
k0 = 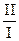 =
= 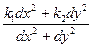 .
.
Нормальная кривизна в направлении оси х, так как имеем отношение (dx: 0) равна k1, а в направлении оси у имеем отношение (0: dy), и нормальная кривизна равна k2.
Таким образом, коэффициенты k1 и k 2 являются главными нормальными кривизнами поверхности F в точке О.
Определение 3. Числа H = 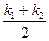 и K = k1 k2 называют, соответственно, средней и гауссовой кривизной поверхности F в точке О.
и K = k1 k2 называют, соответственно, средней и гауссовой кривизной поверхности F в точке О.
Теорема. Главные нормальные кривизны поверхности F в точке О с точностью до знака совпадают со значениями кривизны кривых главных нормальных сечений.
Доказательство. Пусть g1 , g2 - кривые главных нормальных сечений. Тогда
g1: 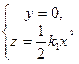 , что равносильно системе
, что равносильно системе 
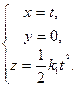
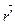 (1; 0; k1t),
(1; 0; k1t), 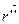 (0; 0; k1).
(0; 0; k1).
Так как
k = 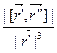 ,
,
то в точке О (при t = 0) получим:
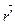 (1; 0; 0),
(1; 0; 0), 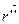 (0; 0; k1).
(0; 0; k1).
[  =
= 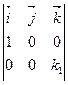 = - k1
= - k1 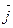 .
.
Так как
| [  | = |k1|, |
| = |k1|, | 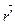 | = 1,
| = 1,
то
k = | k1|.
Аналогично для кривой g2 получим:
g2: 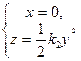 ,
,
что равносильно системе
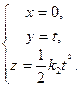
Далее, продолжая по предыдущей схеме, находим:
k = | k2|.
Теорема доказана.
 2015-05-13
2015-05-13 2620
2620
