Определение 1. Две поверхности F1 и F2 называются изометричными, если между их точками может быть установлено такое взаимно однозначное соответствие, при котором соответствующие кривые на поверхностях F1 и F2 имеют одинаковые длины.
Про изометричные поверхности говорят, что одна из них получена изгибанием другой. Таким образом, изгибание поверхности – это деформация, при которой не изменяются длины кривых на поверхности.
Следующие рисунки показывают изгибание плоскости в двугранный угол, а далее в параболический цилиндр и изгибание трёхгранного угла в коническую поверхность, которая имеет такую же развёртку в плоский угол, что и данный трёхгранный угол.

Теорема 1. Пусть поверхности F и F  определены регулярными векторными функциями
определены регулярными векторными функциями 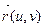 и
и 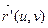 , для которых порядок регулярности к ≥ 1, с одной и той же областью определения Q. Если коэффициенты первых квадратичных форм поверхностей F и F
, для которых порядок регулярности к ≥ 1, с одной и той же областью определения Q. Если коэффициенты первых квадратичных форм поверхностей F и F  в области Q равны, то есть для всех
в области Q равны, то есть для всех 
Е  = Е¢
= Е¢  , F
, F  = F¢
= F¢  , G
, G  = G¢
= G¢  , (1)
, (1)
то поверхности F и F¢ изометричны.
Доказательство. Будем считать соответствующими точками поверхностей F и F  точки М
точки М  и
и 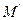
 , имеющие одни и те же координаты
, имеющие одни и те же координаты  .
.
Пусть гладкая кривая g на F задаётся уравнениями:
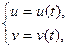 t Î (
t Î (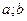 ).
).
Тогда соответствующая ей кривая g¢ на F  задаётся теми же уравнениями. Поэтому, в силу равенств (1)
задаётся теми же уравнениями. Поэтому, в силу равенств (1)
s (g) = 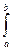
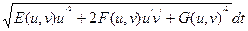 =
=
= 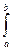
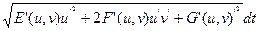 = s (g¢),
= s (g¢),
откуда и следует изометричность поверхностей F и F¢.
Теорема 2. Пусть поверхности F и F  определены регулярными векторными функциями
определены регулярными векторными функциями 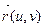 и
и 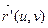 , для которых порядок регулярности к ≥ 1 с одной и той же областью определения Q. Тогда если их точки, имеющие одинаковые внутренние координаты
, для которых порядок регулярности к ≥ 1 с одной и той же областью определения Q. Тогда если их точки, имеющие одинаковые внутренние координаты  , соответствуют друг другу по изометрии, то коэффициенты первых квадратичных форм поверхностей F и F
, соответствуют друг другу по изометрии, то коэффициенты первых квадратичных форм поверхностей F и F  равны.
равны.
Доказательство. Нам надо доказать, что
Е  = Е¢
= Е¢  , F
, F  = F¢
= F¢  , G
, G  = G¢
= G¢  .
.
Рассмотрим три пары соответственных кривых, заданных уравнениями:
g ÎF и g¢Î F¢: 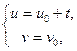 tÎ(
tÎ(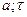 ) Þ
) Þ 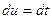 ,
, 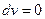 .
.
g1 ÎF и g¢1 Î F¢: 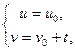 tÎ(
tÎ(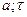 ) Þ
) Þ 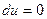 ,
, 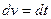 .
.
g2 ÎF и g¢2 Î F¢: 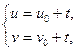 tÎ(
tÎ(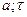 ) Þ
) Þ 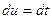 ,
, 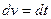 .
.
Мы рассматриваем переменную t из промежутка (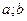 ).
).
Согласно условию теоремы, соответствующие друг другу по изометрии кривые имеют равные длины, т.е. выполняется равенство
s(g) = s(g¢), s(g1) = s(g¢1), s(g2) = s(g¢2),
s(g) = 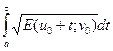 =
= 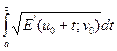 = s(g¢). (2)
= s(g¢). (2)
Так как равенство (2) верно для любого 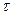 Î (
Î (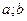 ), то равны подинтегральные выражения
), то равны подинтегральные выражения 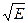 =
= 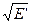 , а следовательно,
, а следовательно,
Е  = Е¢
= Е¢  . (3)
. (3)
Применяя такие же рассуждения к кривым g1 ÎF и g¢1 Î F¢, получим:
G  = G¢
= G¢  . (4)
. (4)
Учитывая, что Е = Е¢ и G = G¢, рассмотрим третью пару кривых g2 ÎF и g¢2 Î F¢.
Получим равенство:
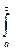
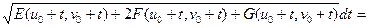
= 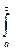
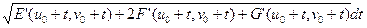 .
.
Равенство верно для любого 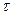 Î (
Î (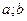 ). Поэтому равны подинтегральные выражения
). Поэтому равны подинтегральные выражения
Е  +2F
+2F  +G
+G  = E′
= E′  +2F′
+2F′  +G′
+G′  .
.
Из этого равенства, учитывая равенства (3) и (4), получим, что
F  = F¢
= F¢  . (5)
. (5)
Теорема доказана.
 2015-05-13
2015-05-13 2185
2185
