Теорема Эйлера. Экстремальные свойства главных направлений

Ранее мы находили из уравнения соприкасающегося параболоида первую и вторую квадратичные формы:

I = dx² + dy ²

и

II= k₁ dx² + k₂dy².

Нормальная кривизна соприкасающегося параболоида и поверхности в точке О в направлении (dx: dy) имеет вид:

k₀ = = .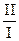

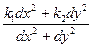Запишем это выражение в виде

k₀ = k₁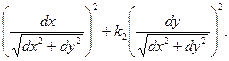

Тогда если обозначить через j угол, который образует направление (dx: dy) с направлением оси х (т.е. с первым главным направлением), то можно обозначить:

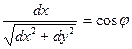и .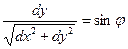

Учитывая эти разложения, получим так называемую формулу Эйлера:

k₀ = k₁ cos²j + k₂ sin²j.

Мы доказали теорему Эйлера.

Теорема 1. Нормальная кривизна k₀ в точке О поверхности F в направлении, составляющем угол j с первым главным направлением, равна:

k₀ = k₁ cos²j + k₂ sin²j,

где k₁ и k₂ – главные нормальные кривизны поверхности F в точке O.

Теорема 2. В главных направлениях С²- гладкой поверхности в данной точке нормальные кривизны достигают экстремумов.

Доказательство. Рассмотрим два случая.

1) k₁ ¹ k₂. Пусть для определённости k₁ > k₂. Тогда для направления, составляющего угол j с первым главным направлением, имеем:

k₀ = k₁ cos²j + k₂ sin²j = k₁ – (k₁ - k₂) sin²j.

Отсюда ясно, что k₀ как функция j имеет ровно два экстремальных значения: наибольшее значение, равное k₁, достигается при j = 0 или p; наименьшее значение, равное k₂, достигается при j = 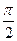или .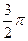

2) k₁ = k₂. Тогда для любого направления имеем:

k₀ = k₁(cos²j + sin²j) = k₁,

k₀ = k₁ = k₂,

то есть все нормальные кривизны поверхности в данной точке равны. Любое направление можно считать главным.

Теорема доказана.