Гауссовой кривизны

Сфера радиуса R есть пример поверхности постоянной положительной гауссовой кривизны К = 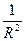> 0.

Плоскость есть пример поверхности нулевой гауссовой кривизны.

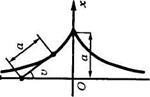
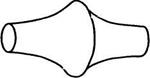
Простейшей поверхностью постоянной отрицательной гауссовой кривизны является псевдосфера. Эта поверхность получается вращением трактрисы вокруг своей асимптоты. Характерным свойством трактрисы является то, что длина отрезка касательной от точки касания до ее оси постоянна. Если выбрать в качестве оси трактрисы ось Z, а величину угла между осью и касательной взять за параметр v, то в плоскости Оxz уравнение трактрисы имеет вид:

.

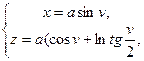
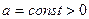Рассматривая кривую как меридиан, можно получить уравнение поверхности вращения вокруг оси Z, т.е. псевдосферы

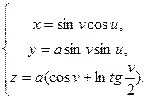
Из уравнения можно найти гауссову кривизну псевдосферы:

К = − .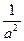

Дифференциальная геометрия позволяет по-новому взглянуть на три уже хорошо известные нам геометрии: евклидову планиметрию, планиметрию Лобачевского и геометрию сферы. Оказывается, что любая поверхность постоянной гауссовой кривизны «в малом» изометрична одной из перечисленных планиметрий.

Так, изучив внутреннюю геометрию сферы, мы получим представление о внутренней геометрии любой поверхности постоянной положительной гауссовой кривизны. Поверхности нулевой гауссовой кривизны локально изометричны евклидовой плоскости, а поверхности постоянной отрицательной гауссовой кривизны «в малом» имеют геометрию плоскости Лобачевского.

РЕШЕНИЕ НУЛЕВОГО ВАРИАНТА