Найти уравнения касательной плоскости и нормали в точке ( ), первую и вторую квадратичные формы поверхности, заданной уравнением
), первую и вторую квадратичные формы поверхности, заданной уравнением 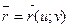 , если
, если 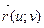 =
= 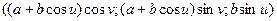 .
.
Решение. Находим векторы 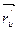 и
и 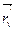 .
.
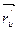 (-bcosvsinu; -bsinvsinu; bcosu),
(-bcosvsinu; -bsinvsinu; bcosu),
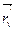 (- (
(- (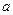 +bcosu)sinv; (
+bcosu)sinv; (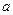 +bcosu)cosv; 0).
+bcosu)cosv; 0).
По условию задачи мы должны найти уравнение касательной плоскости при 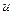 =
= 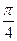 ,
, 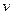 =
= 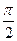 , то есть в точке М0 (0;
, то есть в точке М0 (0; 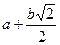 ;
; 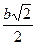 ). Учитывая, что
). Учитывая, что 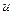 =
= 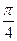 ,
, 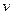 =
= 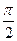 , получим:
, получим:
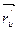 (0; -
(0; - 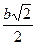 ;
; 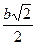 ),
),
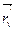 (- (
(- (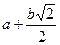 ); 0; 0).
); 0; 0).
Находим уравнение касательной плоскости в точке М0 (0; 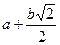 ;
; 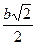 ):
):
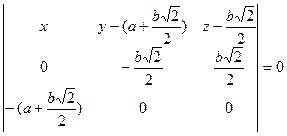 Û
Û 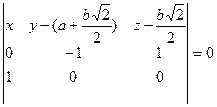 Û
Û 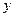 – (
– (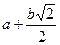 ) +
) + 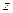 –
– 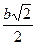 = 0 Û
= 0 Û 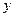 +
+ 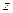 – (
– (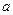 +
+ 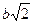 ) = 0.
) = 0.
Уравнение касательной: 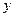 +
+ 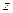 – (
– (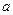 +
+ 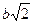 ) = 0.
) = 0.
Находим уравнение нормали в точке М0 (0; 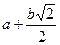 ;
; 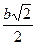 ). Из уравнения касательной плоскости находим нормальный вектор к поверхности в точке М0:
). Из уравнения касательной плоскости находим нормальный вектор к поверхности в точке М0: 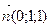 . Вектор
. Вектор 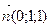 будет направляющим вектором искомой нормали. Находим канонические уравнения нормали к поверхности:
будет направляющим вектором искомой нормали. Находим канонические уравнения нормали к поверхности:
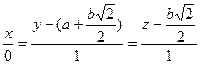 .
.
Находим коэффициенты первой квадратичной формы поверхности:
E = 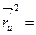
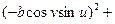
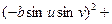
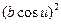 =
= 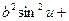 .
. 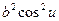 =b2.
=b2.
F = 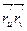 = 0.
= 0.
G = 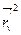 =
= 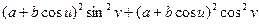 =
= 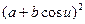 .
.
I = b2du2 + 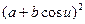 dv2.
dv2.
E G – F2 = 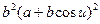 .
.
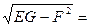
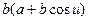 .
.
Находим вторые частные производные:
 ,
,
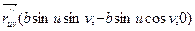 ,
,
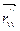 (- (
(- (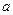 +bcosu)сosv; -(
+bcosu)сosv; -(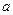 +bcosu)sinv; 0).
+bcosu)sinv; 0).
Ранее мы получили формулы для вычисления коэффициентов второй квадратичной формы:
L = 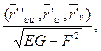 M =
M = 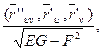 N =
N = 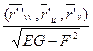 .
.
(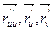 ) =
) = 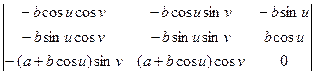 = =
= = 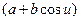
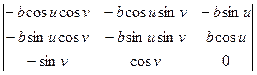 =
= 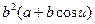 .
.
L = 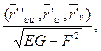 =
= 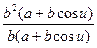 =
= 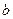 .
.
L = 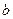 .
.
(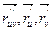 ) =
) = 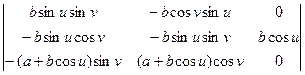 = 0.
= 0.
М = 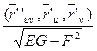 = 0.
= 0.
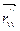 (- (
(- (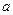 +bcosu)сosv; -(
+bcosu)сosv; -(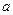 +bcosu)sinv; 0).
+bcosu)sinv; 0).
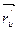 (-bcosvsinu; -bsinvsinu; bcosu),
(-bcosvsinu; -bsinvsinu; bcosu),
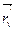 (- (
(- (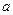 +bcosu)sinv; (
+bcosu)sinv; (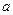 +bcosu)cosv; 0).
+bcosu)cosv; 0).
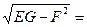
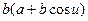
(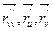 ) =
) = 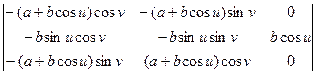 =
=
= 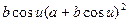 .
.
N = 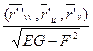 =
= 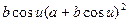 :
: 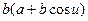 =
= 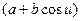
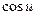 .
.
II = bdu2 + 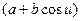
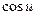 dv2.
dv2.
Ответ: y + z – (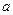 +
+ 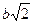 ) = 0,
) = 0, 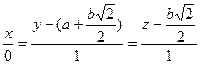 ,
,
I = b2du2 + 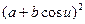 dv2, II = bdu2 +
dv2, II = bdu2 + 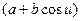
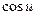 dv2.
dv2.
 2015-05-13
2015-05-13 765
765








