Найти единичные векторы репера Френе 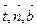 , уравнение касательной, кривизну и кручение кривой
, уравнение касательной, кривизну и кручение кривой 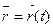 в данной точке t0 =
в данной точке t0 = 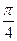 , если
, если
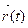 = cos3t
= cos3t 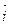 +sin3t
+sin3t 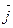 +cos2t
+cos2t 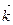 .
.
Решение. Предварительно находим первые, вторые и третьи производные заданной функции: 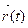 = cos3t
= cos3t 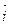 +sin3t
+sin3t 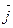 +cos2t
+cos2t 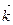 .
.
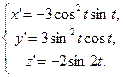
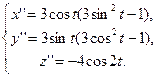
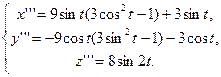
Находим первые, вторые и третьи производные в данной точке t0 = 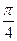 .
.
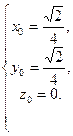
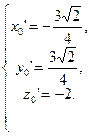
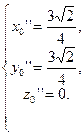
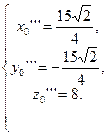
Находим единичные векторы репера Френе 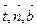 .
.
Единичный касательный вектор 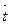 можно получить, разделив касательный вектор
можно получить, разделив касательный вектор 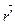 на его длину. Находим:
на его длину. Находим:
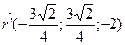 , |
, | 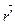 | =
| = 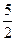 ,
,
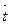 =
= 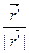 = (
= (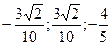 ).
).
Ранее мы показали, что направление бинормали можно задать вектором 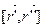 , так как
, так как 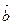 || [
|| [ 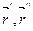 ]. Поэтому полагаем
]. Поэтому полагаем
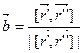 .
.
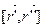 =
= 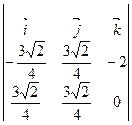 =
= 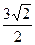
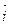 -
- 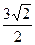
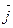 -
- 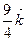 .
.
Так как | 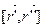 | =
| = 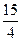 , то
, то
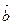 = (
= (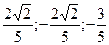 ).
).
Далее находим вектор 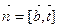 .
.
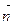 =
= 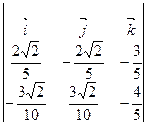 =
= 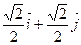 ,
,
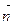 (
(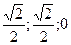 ).
).
Находим уравнение касательной, кривизну и кручение кривой 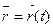 в данной точке t0 =
в данной точке t0 = 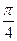 .
.
Касательная прямая определена точкой М0 (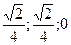 ) и направляющим вектором
) и направляющим вектором 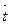 (
(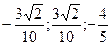 ).
).
Для составления уравнения можно выбрать вектор, коллинеарный вектору 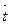 , например, вектор
, например, вектор 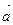 (3
(3 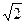 ; -3
; -3 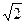 ; 8).
; 8).
Поэтому получим канонические уравнения касательной:
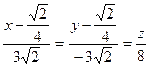 .
.
Находим кривизну кривой по формуле
k = 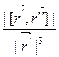 .
.
Ранее мы находили
| 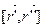 | =
| = 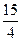 , |
, | 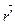 | =
| = 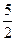 .
.
Следовательно,
k = 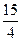 : (
: (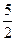 )3 =
)3 = 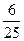 .
.
Кручение кривой находим по формуле
t(t) = 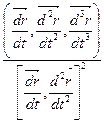 .
.
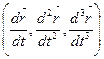 =
= 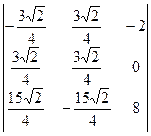 = - 9 +11,25 -11,25 – 9 = -18.
= - 9 +11,25 -11,25 – 9 = -18.
Так как | 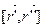 | =
| = 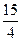 , то t(t) = -18: (
, то t(t) = -18: (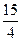 )2 = -
)2 = - 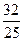 .
.
Ответ: 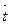 (
(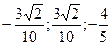 ),
), 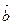 (
(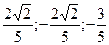 ),
), 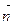 (
(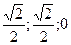 ),
),
k = 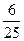 , t(t) = -
, t(t) = - 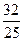 .
.
 2015-05-13
2015-05-13 2984
2984








