Задание 1
Найти естественную параметризацию кривой, заданной векторной функцией 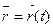 на промежутке (- ¥; +¥), если
на промежутке (- ¥; +¥), если
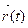 = cos3t
= cos3t 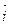 +sin3t
+sin3t 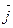 +cos2t
+cos2t 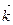 .
.
Решение. Находим длину дуги кривой с фиксированным одним концом. Предполагаем, что эта дуга соответствует промежутку tÎ [0; t].
Находим производные координатных функций:
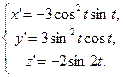
S = 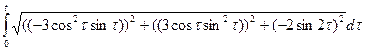 =
=
= 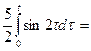 −
− 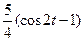 ,
,
S = − 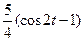 .
.
Находим:
cos2t = 1 − 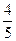 s, t =
s, t = 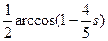 .
.
Подставляя полученное выражение для t в данное по условию уравнение кривой, находим уравнение кривой в естественной параметризации:
x = cos3(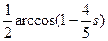 ) = (1 −
) = (1 − 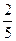 s
s 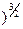 ,
,
y = sin3(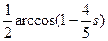 ) = (
) = (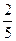 s
s 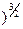 ,
,
z = cos arccos 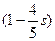 ) = 1-
) = 1- 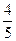 s.
s.
Ответ: 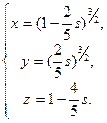
 2015-05-13
2015-05-13 649
649








