А 1. Отображение 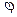 : (
: (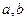 )
) 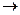 E3 называется непрерывным в точке х0
E3 называется непрерывным в точке х0 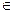 (
(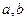 )
)
1) если для любого числа 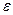 > 0 из условия х
> 0 из условия х 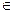 (
(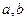 ) следует, что
) следует, что
расстояние от точки 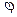 (х) до точки
(х) до точки 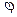 (х0) меньше
(х0) меньше 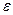
2) если оно является биекцией
3) если оно непрерывно в каждой точке интервала (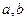 )
)
4) если 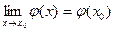
5) другой ответ
А 2. Множество 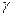 точек пространства называется простой кривой
точек пространства называется простой кривой
1) если это множество является локально топологическим образом элементарной кривой
2) если каждая точка М Î g имеет такую окрестность UM в Е3, что 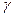 Ç UM = gМ является элементарной кривой
Ç UM = gМ является элементарной кривой
3) если это множество является образом интервала при гомеоморфизме
4) если это множество является образом интервала при непрерывном отображении
5) другой ответ
А 3. Кривая 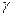 называется регулярной класса Ск
называется регулярной класса Ск
1) если существует параметризация 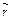 (t), что каждая координатная функция вектора
(t), что каждая координатная функция вектора 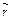 (t) принадлежит классу регулярности Ск и
(t) принадлежит классу регулярности Ск и 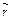 ’(t)
’(t) 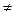
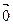
2) если для любой ее параметризации 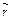 (t) каждая координатная функция принадлежит классу регулярности Ск и
(t) каждая координатная функция принадлежит классу регулярности Ск и 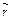 ’(t)
’(t) 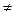
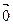
3) если существует такая ее параметризация, что каждая координатная функция вектора 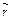 (t) принадлежит классу регулярности Ск
(t) принадлежит классу регулярности Ск
4) если существует такая ее параметризация 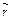 (t), что
(t), что 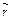 ’(t)
’(t) 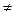
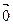
А 4. Касательной к кривой g: 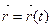 , (
, (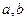 ) в точке М (t) Î g называется
) в точке М (t) Î g называется
1) прямая (М (t), М′(t+Dt)), если t, t+Dt Î (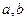 )
)
2) предел прямых (М (t), М¢(t+Dt)), t, t+Dt Î (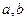 ) при Dt ® 0, (если он существует)
) при Dt ® 0, (если он существует)
3) предел прямых (М (t), М¢ (t+Dt)), t, t+Dt Î (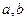 ) при Dt ® 0
) при Dt ® 0
4) прямая, которая задана точкой М (t) и направляющим вектором 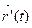
5) другой ответ
А5. Пусть 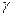 - к -регулярная кривая (к ≥ 2),
- к -регулярная кривая (к ≥ 2), 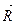 =
= 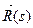 -ее естественная параметризация. М(s), М(s+Ds) - точки кривой g,
-ее естественная параметризация. М(s), М(s+Ds) - точки кривой g, 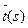 и
и 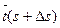 - касательные векторы к кривой g в этих точках. j(s, Ds) - угол между этими векторами. Кривизной k (s) кривой g в точке М(s) называется
- касательные векторы к кривой g в этих точках. j(s, Ds) - угол между этими векторами. Кривизной k (s) кривой g в точке М(s) называется
1) предел (если он существует) отношения 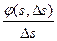 при Ds ®0
при Ds ®0
2) отношение 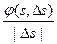
3) предел (если он существует) отношения 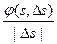 при Ds ®0
при Ds ®0
4) предел отношения 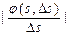 при Ds ®0
при Ds ®0
5) другой ответ
А 6. Укажите верные равенства, если k (s) - кривизна кривой, 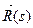 - естественная параметризация кривой,
- естественная параметризация кривой, 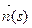 - нормальный вектор,
- нормальный вектор, 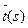 - касательный вектор
- касательный вектор
1) к(s)= 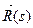 2) к(s)=
2) к(s)= 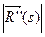 3)
3) 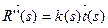
4) 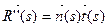 5)
5) 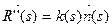
А 7. Плоскость, заданная точкой М0 и векторами 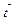 ,
, 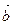 , называется
, называется
1) нормальной плоскостью кривой g в точке М0
2) спрямляющей плоскостью кривой g в точке М0
3) касательной плоскостью кривой g в точке М0
4) соприкасающейся плоскостью кривой g в точке М0
А 8. Прямая, заданная точкой М0 и вектором 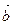 , называется
, называется
1) нормалью к кривой g в точке М0
2) касательной к кривой g в точке М0
3) бинормалью к кривой g в точке М0
4) другое название
А 9. Чтобы существовало кручение кривой g, достаточно следующего условия
1) число 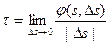 в каждой точке кривой g существует,
в каждой точке кривой g существует,
где 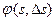 = ± (
= ± (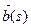 ,Ù
,Ù 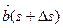 ),
), 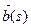 - бинормальный вектор
- бинормальный вектор
2) g - к-регулярная кривая
3) g - к -регулярная кривая заданна естественной параметризацией 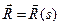 , s Î(0,S), к³3
, s Î(0,S), к³3
4) g - к -регулярная кривая в каждой своей точке имеет кривизну k(s) 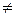 0
0
5) другой ответ
А 10. Найти координатные линии поверхности, заданной функцией
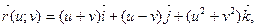 где (u;v)ÎR2
где (u;v)ÎR2
1) gu: 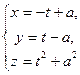 gv:
gv: 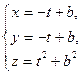 2) gu:
2) gu: 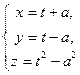 gv:
gv: 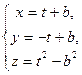
3) gu: 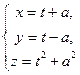 gv:
gv: 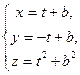 4) gu:
4) gu: 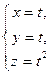 gv:
gv: 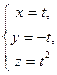
5) другой ответ.
А 11. Первой квадратичной формой поверхности, заданной гладкой параметризацией 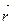 =
= 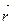 (u, v) называется
(u, v) называется
1) полный квадрат первой производной вектор-функции 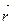 (u, v)
(u, v)
2) I = 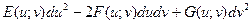 , где Е =
, где Е = 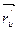 2, F =
2, F = 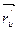
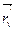 , G =
, G = 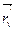 2
2
3) I = 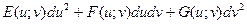 , где Е =
, где Е = 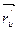 2, F =
2, F = 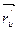
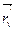 , G =
, G = 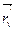 2
2
4) квадрат полного дифференциала 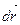 вектор-функции
вектор-функции 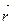 (u, v)
(u, v)
5) другой ответ
А 12. Второй квадратичной формой поверхности F называется
1) II = 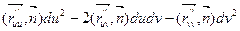
2) скалярное произведение II =(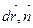 ), где
), где 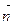 - нормаль к поверхности F
- нормаль к поверхности F
3) II = 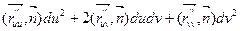
4) скалярное произведение II = (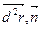 ), где
), где 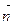 - нормаль к поверхности F, а
- нормаль к поверхности F, а 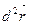 - второй дифференциал вектор-функции
- второй дифференциал вектор-функции 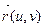
5) другой ответ
А 13. Укажите коэффициент L второй квадратичной формы поверхности
1) 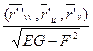 2)
2) 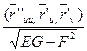 3)
3) 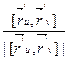 4)
4) 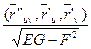 5) другой ответ
5) другой ответ
В1. Записать в естественной параметризации уравнение кривой
g: 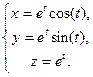 tÎ R.
tÎ R.
В2. Найти вектор 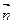 репера Френе кривой g:
репера Френе кривой g: 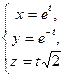 в точке, соответствующей параметру t = 0
в точке, соответствующей параметру t = 0
В3. Составить уравнение касательной плоскости к поверхности, заданной уравнением xyz = 1, параллельной плоскости x + y + z = 1
В4. Найти первую квадратичную форму поверхности 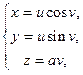
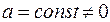
| № A | Номера заданий | ||||||||||||
| Отв. | 2,5 |
СПИСОК ЛИТЕРАТУРЫ
1. Александров А.Д., Нецветаев Н.Ю. Геометрия. – М.: Наука, 1990. –672 с.
2. Аминов Ю.А. Свойства в целом кривых в трехмерном евклидовом пространстве, связанные с кручением // Укр. геом. сб. – 1973. – Вып. 14. – С. 3 – 10.
3. Аминов Ю.А. Дифференциальная геометрия и топология кривых. – М.: Наука, 1987. –160 с.
4. Атанасян Л.С., Базылев В.Т. Геометрия. Ч.2. – М.: Просвещение, 1987. – 351 с.
5. Берман Г.Н. Циклоида. – М.: Наука, 1980. – 112 с.
6. Беклемишева Л.А. и др. Сборник задач по аналитической геометрии: Учеб. пособие. – М., 2003.
7. Бортаковский А.С., Пантелеев А.В. Аналитическая геометрия в примерах и задачах: Учеб. пособие. – М.: Высшая школа, 2005.
8. Вернер А.Л., Кантор Б.Е. Элементы топологии и дифференциаль-
ной геометрии. – М.: Просвещение, 1985. – 113 с.
9. Вернер А.Л., Кантор Б.Е., Франгулов С.А. Геометрия.Ч.2. – СПб., 1997.
10. Гильберт Д., Кон-Фоссен С. Наглядная геометрия. – М.: Наука, 1981. – 352 с.
11. Дубровин Б.А.,Новиков С.П., Фоменко А.Т. Современная геометрия. – М.: Наука, 1986. – 759 с.
12. Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. – М., 2004. – 464 с.
13. Ефимов Н.В. Высшая геометрия: Учебник для вузов. –.М.: Физматлит, 2003. – 584 с.
14. Жаферов А.Ф. Геометрия: В 2 ч. Ч.1. – Новосибирск: Сиб.унив.изд-во, 2002. – 271 с.
15. Жаферов А.Ф. Геометрия: В 2 ч. Ч.2. – Новосибирск: Сиб.унив.изд-во, 2003. – 267 с.
16. Новиков С.П., Фоменко А.Т. Элементы дифференциальной геометрии и топологии: Учебник для университетов. – М.: Наука, 1987. – 432 с.
17. Кон-Фоссен С. Некоторые вопросы дифференциальной геометрии в целом. – М.: Физматгиз, 1959.
18. Кобояси Ш., Номидзу К. Основы дифференциальной геометрии: В 2 т.– М.: Наука,1981. Т.1– 344 с.; Т.2 – 314 с.
19. Рохлин В.А., Фукс Д.Б. Начальный курс топологии. М.: Наука, 1977. – 488 с.
20. Розендорн Э.Р. Задачи по дифференциальной геометрии. – М.: Наука, 1978. – 64 с.
21. Маркушевич А.И. Замечательные кривые. – М.: Наука, 1971.–48 с.
22. Сантало Л. Интегральная геометрия и геометрические вероятности. – М.: Наука,1983. – 358 с.
24. Погорелов А.В. Геометрия. – М.: Наука, 1983. – 288 с.
25. Погорелов А.В. Дифференциальная геометрия. – М.: Наука,1969. – 176 с.
26. Позняк Э.Г., Шикин Е.В. Дифференциальная геометрия. – М.: МГУ, 1990. –384 с.
27. Шилов Г.Е. Математический анализ. Функции одного переменного. Ч. – 3. – М.: Наука,1970. – 352 с.
28. Шварц Дж. Дифференциальная геометрия и топология. –Новокузнецк: НФМИ, 2000.
29. Фоменко А.Т. Дифференциальная геометрия и топология. Дополнительные главы. – М.: Изд-во Моск. ун-та, 1983. – 216 с.
 2015-05-13
2015-05-13 561
561







