Пересечение плоскостей и поверхностей

Решение задачи №7

Предварительные замечания.

Так как, согласно условию, во вза-имнодействие вступают плоскость a и поверхность Ф, то на форму его резу-льтата влияет как их положение отно-сительно П₁ и П₂, так и их взаимное ра-сположение. При этом разнообразие условий конкретных задач определя-ется видами пересекаемых поверхнос-тей.

Задача №7.1. Построить двухкар-тинный комплексный чертёж линии пересечения призматической поверх-ности Ф и плоскости a;

Задача №7.2. Построить двухкар-тинный комплексный чертёж линии пересечения цилиндрической поверх-ности Ф и плоскости a;

Задача №7.3. Построить двухрар-тинный комплексный чертёж линии пересечения пирамидальной поверхно-сти Ф и плоскости a;

Задача №7.4. Построить двухкар-тинный комплексный чертёж линии пересечения конической поверхности Ф и плоскости a;

Задача №7.5. Построить двухкар-тинный комплексный чертёж линии пересечения плоскости a и поверхно-сти вращения второго порядка.

Решение задачи №7.1

Рассмотрение различных сочета-ний положений поверхности и плоскос-ти требует применения системной та-блицы Кэли (рис. 16.4).

В связи с тем, что рассматриваются преимущественно двухкартинные комп-

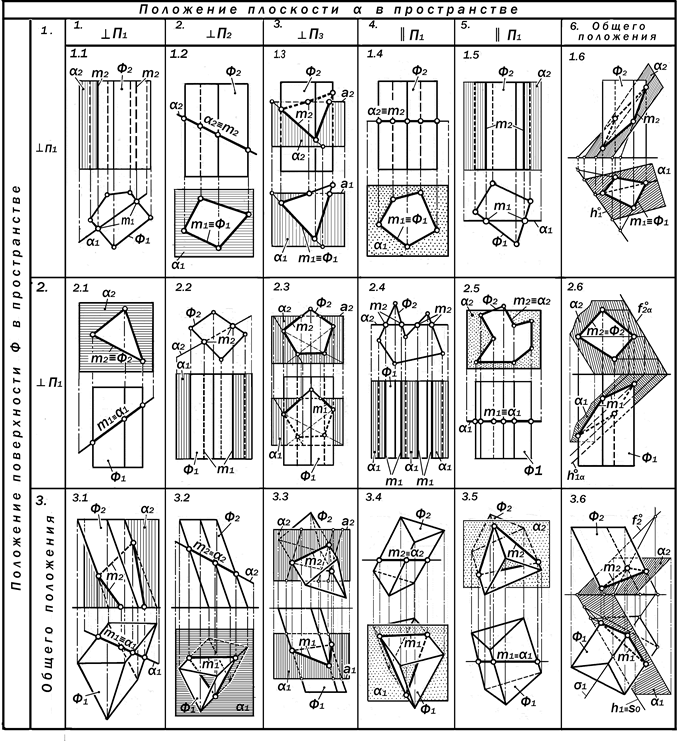Рис. 16. 4. Варианты решения

позиционных задач на пересечение

плоскостей с призматическими

поверхностями

лексные чертежи этих сочетаний, то в эту таблицу условно не внесены про-фильные плоскости уровня и профиль-но-проецирующие поверхности, требу-ющие построения трёхкартинных комп-лексных чертежей.

В ы в о д ы и з р е ш е н и я

1. Если плоскость a и поверхность Ф являются проецирующими одного на-правления (п.п. 1.1, 1.5, 2.2 и 2.4), то они пересекаются по прямым m, парал-лельным рёбрам поверхности, одни из

проекций которых являются точкам пе-

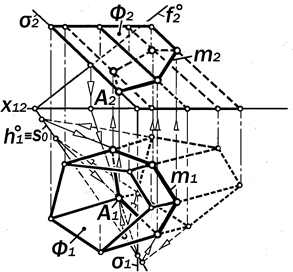Рис. 16.5. Фигура сечения призмы Ф

плоскостью a родственна фигуре её основания

ресечения их вырожденных проекций, а вторые совпадают с направлением ли-ний связи;

2. Если плоскость a и поверхность Ф являются проецирующими разных направлений (п.п. 1.2, 1.4, 2.1 и 2.5), то разноименные проекции m₁ и m₂ ис- комой линии m их пересечения совпа-дают с соответствующими вырожден-ными проекциями данных плоскости a и поверхности Ф, т.е., m₁ º Ф₁, m₂ º a₂.

3. Если плоскость a занимает про-фильно-проецирующее положение, а поверхность Ф – горизонтально-проеци-рующее, то горизонтальная проекция m₁ совпадает с вырожденной в линию проекцией Ф₁ поверхности Ф, а фрон-тальная m₂ строится на основе графи-ческого моделирования отношения при-надлежности фигуры m к плоскости a

(п.п. 1.3, 2.3):

a ^ П₃ Ù Ф ^ П₁ Þ m₁ º Ф₁, m₂ Î a₂.

4. Если плоскость a является прое-цирующей, а поверхность Ф – общего положения, то одна из проекций линии их пересечения совпадает с вырожден-ной в прямую линию проекцией этой плоскости, а вторая проекция строится на основе графического моделирова-ния отношения при-надлежности её то-чек к поверхности Ф (п.п.3.1, 3.4, 3.5);

a ^ П₁ (П₂), а Ф -

о.п. Þ m₁ º a₁,

(m₂ º a₂),

m₂ Î Ф₂, (m₁ Î Ф₁).

5. Если плоско-

сть a - общего по-ложения, а поверх-ность Ф проециру-ющая (п.п.1.6,2.6), то одна из проек-ций линии их пере-сечения совпадает с фигурой вырож-денной проекции поверхности, а её другая проекция строится по прина-

длежности её точек к плоскости a.

a - о.п., Ф ^ П₁ (П₂) Þ m₁ º Ф₁, (m₂ º Ф₂),

m₂ Î a₂ (m₁ Î a₁).

6. Если плоскость a ^ П₃ или обще-

го положения, и поверхность Ф -общего

положения, то решение задачи сводит-ся к построению точек встречи её рёбер

с этой плоскостью (п.п. 3.3, 3.6) (см рис. 10.27).

Следует особо отметить, что фигу-ра сечения поверхности плоскостью

родственна фигуре её основания так как направление родства совпадает с рёбрами поверхности, а осью родства является линия пересечения секущей плоскости с плоскостью основания по-верхности.

Это обстоятельство определяет рациональную технологию графическо-го построения фигуры плоского сечения призматической поверхности по алго-ритму теоремы Дезарга (рис.16.5).

Решение задачи №7.2

Согласно условию, в этой задаче плоскость a пересекается с цилиндри-ческой поверхностью Ф. В отличие от многогранной призматической поверх-ности она является кривой, выступа-ющей как предел, к которому стремится вписанная в неё призматическая пове-рхность при бесконечном увеличении числа её граней.

Отсюда следует, что в сечениях цилиндрических поверхностей плоско-стями, не совпадающими с направле-нием их образующих, всегда будут по-лучаться кривые линии, точками кото-рых позиционно являются точки встре-чи её образующих с секущими плоско-стями.

Так как призматическая поверхно-сть является многогранным прототипом

цилиндрической, то по своему содержа-нию технологии графического построе-ния линии их пересечения плоскостями различного положения принципиально одинаковы, а по форме различаются тем, что в сечении призматической по-верхности получается плоская ломаная линия, а в сечении цилиндрической поверхности – плоская кривая линия.

Отсюда следуют общие в ы в о д ы:

1. Линии пересечения цилиндриче-ских поверхностей различного вида и положения в пространстве плоскостями различного положения строятся по точкам встречи последних с необходи-мым и достаточным числом прямоли-нейных образующих этих поверхнос-тей;

2. Точки пересечения с плоскостью

тех образующих поверхности, которые

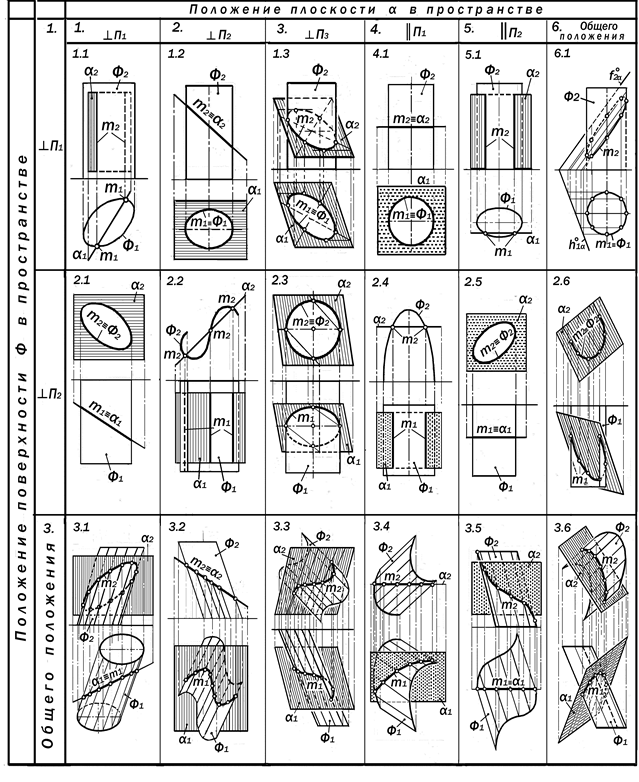Рис. 16.6. Варианты графических

решений позиционных задач на

пересечение плоскости с

цилиндрической поверхностью

рые проецируются в очерки проекций этой поверхности, являются точками исчезновения видимости искомой ли-нии пересечения. Эти точки относятся к числу опорных, равно как наивысшие и наинизшие, а также наилевейшие и наи

правейшие точки проекции этой линии.

3. Выводы, вытекающие из анализа решения задачи №7.1, справедливы для приведенных на рис. 16.6 решений задачи №7.2.

4. Фигура сечения плоскостью ци- линдрической поверхности родственна

фигуре её основания.

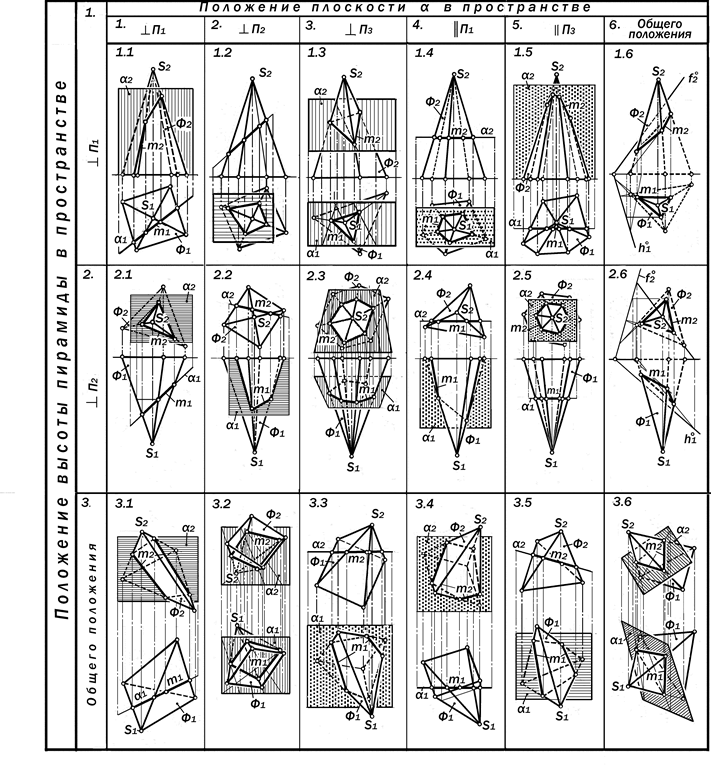Рис. 16.7. Варианты решения позиционных задач на пересечения

плоскости с пирамидальной

поверхностью

Р е ш е н и е з а д а ч и № 7.3

Согласно условию, в этой задаче плоскость a пересекается с поверхнос-тью пирамиды Ф. В отличие от призма-тической пирамидальная поверхность имеет собственную вершину и две по-

лы, состоящие из треугольных граней.

В результате пересечения любой пирамидальной поверхности плоскос-тью, не проходящей через вершину, но пересекающей все рёбра, получается

плоский многоугольник, вершинами которого являются точки встречи этих рёбер с секущей плоскостью.

Рис. 16.8. Варианты решения

позиционных задач на пересечение

плоскости с конической

поверхностью

Р е ш е н и е з а д а ч и №7.4

(рис. 16.8)

Согласно условию, в этой задаче плоскость a пересекает коническую по-верхность Ф. Так как эта поверхность

прямолинейчата и имеет две полы, то

по содержанию решения эта задача не

отличается от вышеприведенных, так

как искомые линии их пересечения ст-роятся по точкам встречи образующих с секущей плоскостью. Различия этих

линий по форме определяются особен-ностями расположения секущей плос-кости по отношению к образующим ли-

ниями поверхности (см. рис.12.13).

Если поверхность прямого круго-

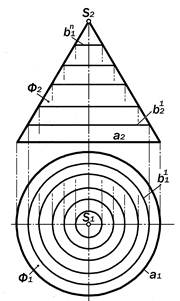Рис. 16.9. Окружности как конические сечения

a

Рис. 16.11. Фрагмент А рис.16.10

вого конуса пересекается плоскостями различного положения, то в результате получаются алгебраические кривые ли-нии второго порядка или коники: окруж-ность, эллипс, парабола и гипербола.

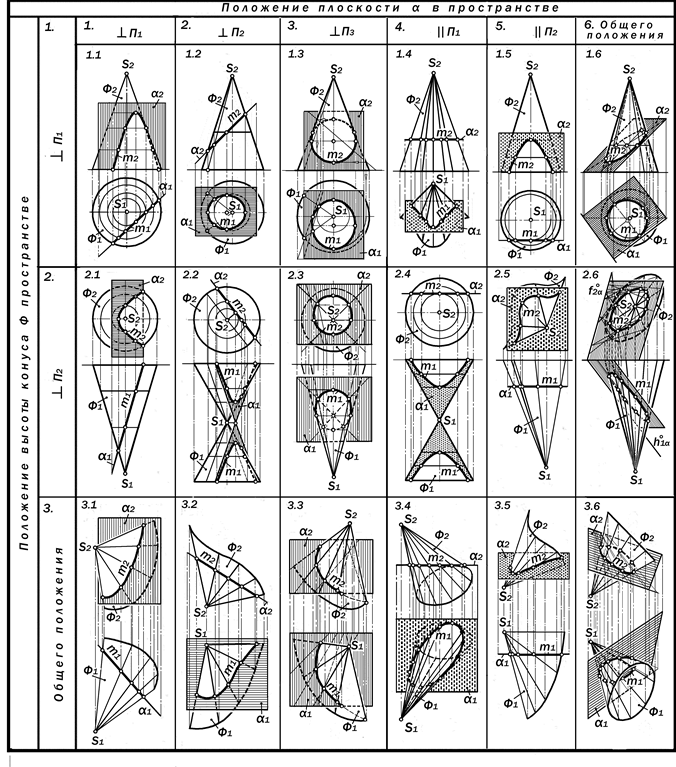
1. Окружность как коническое се-чение лежит в плоскости, перпендику-лярной к оси вращения поверхности Ф и называется её нормальным сечени-ем. В качестве такового, как правило, выступает основание этой поверхности (рис.16.8, п.п. 1.1 -2.5). Последователь-ные сечения плоскостями, параллель-ными плоскости основания, называют-ся параллелями конической поверхнос-ти. Все эти параллели подобны осно-ванию поверхности, а потому подобны друг другу (рис.16.9).

2. Эллипс как коническое сечение лежит в плоскости, пересекающей все образующие одной полы поверхности и не перпендикулярной к оси её враще-ния (рис.16.8, п.п.1.2, 1.3, 1.6, 3.4, 3.6).

Так как эллипс – замкнутая плоская кривая, то её ортогональные проекции строятся по точкам встречи образую-щих поверхности с секущей плоскос-тью (рис.16.10).

Начинать построение проекций эл-липса следует с их опорных точек, к числу которых относятся:

2.1. Вершины А₁ и В₁ как концы бо-льшой оси горизонтальной проекции m₁ искомого эллипса m. Располагаются на горизонтальной проекции u₁ линии наи-большего уклона u секущей плоскости a, проходящей через ось вращения і поверхности Ф и пересекающей в этих точках эту поверхность. Строятся по их проекциям А₂ и В₂, первая из которых является наинизшей, а вторая – наивы - сшей точками фронтальной проекции m₂ искомого эллипса m.

А₂=u₂ (1₂2₂)´ 3₂S₂; B₂ = u₂ (1₂2₂)´ S₂4₂.

2.2. Малая осьC₁D₁ проекции m₁ эл-липса m является горизонталью h плос-кости a, проходящей через середину о его большой оси АВ. Точки C₁ и D₁ определяются в пересечении этой гори-зонтали с параллелью e поверхности конуса Ф на высоте точки о.

C₁D₁ = h₁ ´ e₁.

2.3.По осям А₁В₁ и C₁D₁ cтроится m₁

по графическому алгоритму рис.12.26.

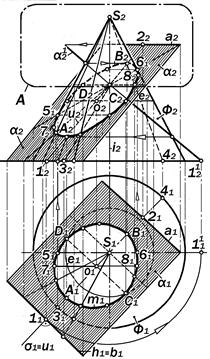Рис. 16.10. Ортогональные проекции эллипса как конического сечения

Горизонтальная проекция m₁ линии m полностью видима.

2.4. Фронтальная проекция m₂ ли-нии m видима не полностью. Точки 5₂ и 6₂ исчезновения её видимости принад-лежат её очерковым образующим и ст-роятся по горизонтальным проекциям 5₁ и 6₁ точек пересечения m₁ с проекци-ей главного меридиана поверхности Ф.

2.5. Точки касания 7₁ и 8₁ вертика-льных линий связи к линии m₁ называ-ются соответственно её левой и пра-вой точками. Проекции 7₂ и 8₂ точек 7 и 8 линии m являются соответственно наилевейшей и наиправейшей точками фронтальной проекции m₂ искомой ли-нии m.

2.6. Фронтальные проекции А₂В₂ и C₂D₂ большой и малой осей искомого эллипса являются сопряженными диа-метрами его фронтальной проекции m₂ и они этот эллипс задают по графичес-кому алгоритму рис.12.28.

Если плоскость a вращением вокруг оси i повернуть до фронтально-проеци-рующего положения a¹ и вписать над ней в поверхность конуса шар Данделе-на S (см. рис.12.14), то он коснется её в фокусе F¹ искомого эллипса, а плос-кость линии его касания к Ф пересечет a по директрисе d¹ (рис. 16.11).

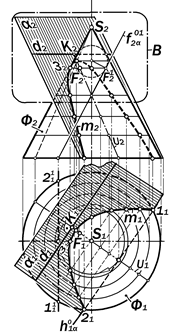Рис. 16.12. Ортогональные проекции параболы как конического сечения

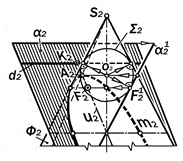Рис. 16.13. Фрагмент В рис. 16.12.

F² и d² симметричны относительно малой оси CD эллипса m и на основе этого строятся их ортогональные про-екции.

3. Парабола как коническое сече-ние лежит в плоскости a, которая па-раллельна одной из образующих пове-рхности Ф. Для задания такого положе-ния этой плоскости её фронтальный след f_2a⁰¹ прежде следует расположить, допустим, параллельно левой очерко-вой образующей (рис.16.12), а затем вращением вокруг оси i еёгоризонталь-ный след h⁰_{1 a} повернуть на некоторый угол, выведя тем самым плоскость a из проецирующего положения в общее.

Построение проекций обыкновен-ных точек параболы следует выпол-нять способом вспомогательных гори-зонтальных плоскостей уровня, кото-рые пересекают плоскость a по её горизонталям, а поверхность Ф – по её соответственным параллелям-окружно-стям.

Изобразительно горизонтальная проекция m₁ параболы m симметрична относительно её оси, совпадающей с горизонтальной проекцией u₁ линии на-ибольшего уклона u плоскости a, про-ходящей через ось вращения поверхно-сти Ф. Проекция m₁ полностью видима.

К числу особых точек параболы от-носятся её вершина А, фокус F и осно-вание К директрисы d.

3.1. Вершина А позиционно является точкой встречи линии u с поверхностью Ф. Её фронтальная проекция А₂ являет-ся наивысшей точкой фронтальной про-екции m₂ параболы m, а горизонталь-ная А₁ принадлежит u₁.

3.2. Фокус F позиционно является точкой касания шара Данделена S к плоскости a. Графически фронтальная проекция о₂ центра о шара S строится как точка пересечения биссектрисы уг-ла между вырожденным следом a₂¹ се-кущей плоскости a и правой очерковой образующей l₂ проекции Ф₂ поверхности Ф с проекцией i₂ осивращения Ф. Про-екция F₂ фокуса F находится на u₂ на уровне её вспомогательной проекции F₂¹ (рис.16.13).

3.3. Основание К директрисы d ле-жит в плоскости кривизны окружности касания шара S к поверхности Ф и в a.

3.4. Точка 3₂ исчезновения видимо-сти фронтальной проекции m₂ парабо-лы m cтроится по её горизонтальнойпроекции 3₁ в пересечении m₁ с гори-зонтальной проекцией главного мери-диана поверхности Ф.

4. Гипербола как коническое сече-ние лежит в плоскости a, параллель-ной двум образующим и пересекающей две полы поверхности Ф. Поэтому кон-структивно она имеет две ветви, две асимптоты и две директрисы.

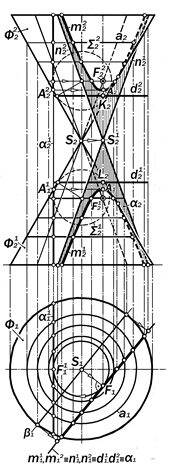Рис.16.14. Ортогональные проекции гиперболы как конического сечения

Так как a^ П₁, то m₁¹,m₁² º n₁¹,n₁² º d¹₁,d²₁ º a₁, где m¹,m², – ветви гипер-болы, d¹ и d² – её директрисы, а n¹, n² –её асимптоты (рис.16.14).

Фронтальные проекции вершин, фо-кусов и директрис строятся при помощи проекций S₂ шаров Данделена, вписан-ных в Ф и касательных к a в фокусах гиперболы. Директрисы принадлежат плоскостям кривизны параллелей каса-ния S к Ф, а асимптоты являются про-екциями на a образующих Ф, парал-лельных a.

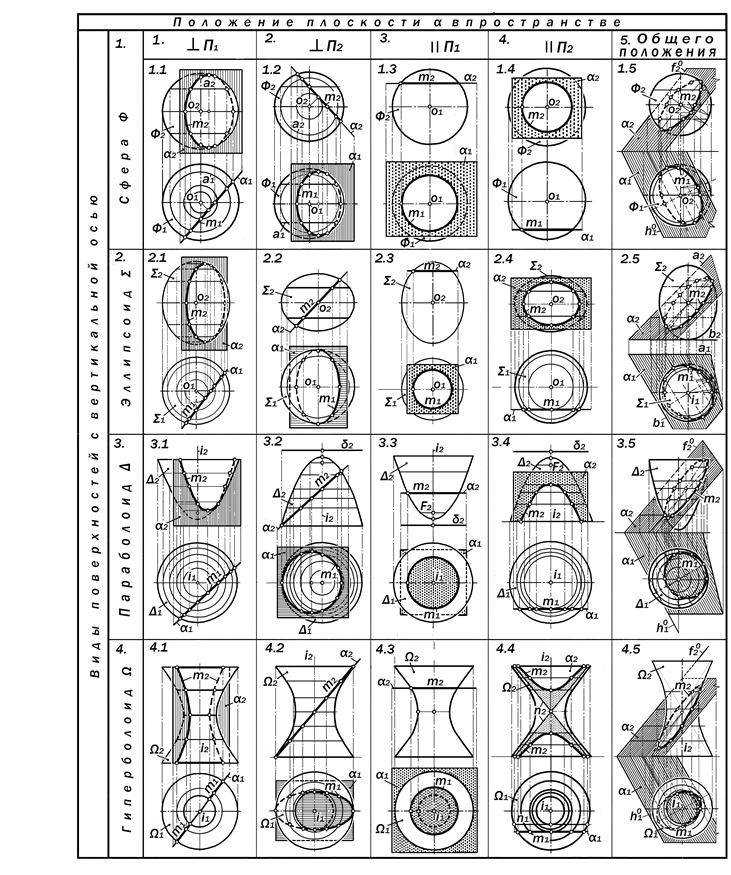Рис.16.15. Варианты решения позиционных задач на пересечение плоскости с поверхностями вращения второго порядка

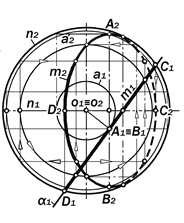Рис. 16.16. Невырожденная

проекция сечения сферы

горизонтально-проецирующей плоскостью

Р е ш е н и е з а д а ч и № 7.5

(рис. 16.15)

Анализ условия:

Согласно условию, в этой задаче плоскость a пересекает поверхности вращения второго порядка – сферу, эл-липсоид, параболоид и однополостный гиперболоид. Так как они образованы вращением кривых линий второго поря-дка, то они криволинейчаты. Поэтому точками искомых линий пересечения этих поверхностей с секущими плос-костями различного положения будут точки встречи с ними соответствующих элементов их линейного каркаса.

Конструктивно линейные каркасы поверхностей вращения любого вида представляют собой пространственные системы их меридианов, компланарных с осью вращения и параллелей-окруж-ностей, плоскости кривизн которых пер-пендикулярны к этой оси.

Позиционно меридианы являются линиями пересечения этих поверхнос-тей плоскостями, проходящими через их ось, а параллели – линиями их пере-сечения плоскостями, перпендикуляр-ными к этой оси.

Так как данные поверхности образу-ются вращением кривых 2-го порядка вокруг их осей симметрии, то их после-довательные положения образуют под-системы конгруэнтных меридианов их линейного каркаса, а точки этих линий в процессе вращения образуют подсисте-мы параллелей-окружностей разного радиуса. Окружности конструктивно яв-ляются наиболее простыми линиями и поэтому для решения поставленной за-дачи целесообразно применять вспо-могательные секущие плоскости уров-ня, перпендикулярные к соответствен-но проецирующим осям заданных по-верхностей вращения

На рис. 16.15 приведены варианты решения позиционных задач на пересе-чение поверхностей вращения 2-го по-рядка, оси которых занимают проециру-ющие положения, с плоскостями как частного, так и общего положения.

Ортогональные проекции искомых линий пересечения обладают рядом конструктивных и изобразительных

свойств.

1. С ф е р а Ф является поверх-ностью постоянной положительной кри-

визны, фигурой любого плоского сече-ния которой является окружность. Поэ-тому:

1.1. Если сфера Ф пересекается плоскостью a частного положения, то одна из проекций искомой окружности является прямой линией, совпадающей с вырожденной проекцией этой плоско-сти (рис.16.15, п.п. 1.1,1.2);

1.2. Если секущая плоскость a за-нимает положение уровня, то проекция m₁₍₂₎ лежащей в ней окружности m на соответствующей плоскости проекций будет окружностью в её натуральную величину (рис.16.15, п.п. 1.3, 1.4);

1.3. Если секущая плоскость a зани-мает то или иное проецирующее поло-жение, то невырожденная проекция фи-гуры сечения является эллипсом, боль-шая ось которого вертикальна, а малая – горизонтальна и совпадает соответ-ственно с вырожденной проекцией эк-ватора (п.1.1) или главного меридиана (п.1.2) пересекаемой сферы Ф.

В связи с тем, что очерки ортого-нальных проекций сферы конгруэнтны, их можно привести в тождественное расположение и на таком совмещенном комплексном чертеже построить невы-рожденную проекцию окружности сече-ния в виде эллипса (рис. 16.16).

К особым точкам этой проекции от-носятся наивысшая А₂ и наинизшая В₂, точки как её вершины, а также точки 1₂ и 2₂ исчезновения её видимости на очерковой линии n₂, которые находятся в проекционной связи с точкой пересе-чения вырожденной проекции m₁ с го-ризонтальной проекцией n₁ главного меридиана сферы.

Фронтальные проекции C₂ и D₂ кон-цов малой оси эллипса m₂ находятся в проекционной связи с точками пересе-чения вырожденной проекции a₁ с про-екцией е₁ экватора е сферы Ф.

Промежуточные точки эллипса m₂ строятся на основе моделирования от-ношения их принадлежности к горизон-талям а поверхности сферы Ф.

1.4. Если сфера пересекается плос-костью общего положения, то окружно-сть сечения, располагаясь в этой плос-кости, проецируется на П₁ и П₂ в эл-липсы m₁ и m₂, параметры которых оп-

ределяются особенностями расположе-ния плоскости a к параллелям сферы.

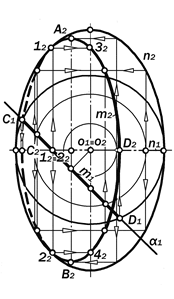Рис.16.17. Невырожденная проекция сечения вытянутого эллипсоида вращения горизонтально-проецирующей плоскостью

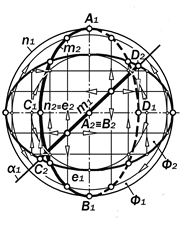Рис.16.18. Невырожденная проекция сечения сжатого эллипсоида вращения фронтально-проецирующей плоскостью

К числу конструктивных свойств ор-тогональных проекций окружности об-щего положения относятся положения их осей, проходящих через проекции её центра. Большие оси её эллиптических проекций совпадают с теми проекциями линий уровня, которые не параллельны оси х₁₂, а малые – совпадают с соответ-ствующими проекциями линий наиболь-шего уклона плоскости её кривизны, перпендикулярными к одноименным проекциям её линий уровня (см. рис. 12.43).

2. Э л л и п с о и д в р а щ е н и я S с вертикальной осью может быть вы-тянутым (рис.16.15, п.п.2.1, 2.3, 2.5) или сжатым (рис.16.15, п.п. 2.2,2.4). По сво-ему содержанию графическое решение задачи на пересечение этих поверхнос-тей с проецирующими плоскостями не отличается от вышеприведенного ре-шения с участием сферы.

Различия между этими решениями по форме определяются конструктив-ными особенностями пересекаемых по-верхностей.

Если совместить проекции о₁ и о₂ центров проекций S₁ и S₂ эллипсоида S, то очерк n₁ его горизонтальной про-екции со следом a₁ секущей плоскости a впишется в очерк n₂ его фронтальной проекции. В итоге получается двойная монопроекция исходного условия, ре-шение которого отличается простотой и компактностью (рис.16.17).

Если секущая плоскость a перпен-дикулярна к оси і вращения вытянутого эллипсоида S, то она пересекает его по

параллели-окружности m соответству-ющего радиуса (рис. 16.15, п.2.3).

Если секущая плоскость a фрон-тальна и не проходит через вертикаль-ную ось вращения сжатого эллипсоида, то фигура фронтальной проекции ли-нии их пересечения подобна очерку фронтальной проекции поверхности и графически строится на основе моде-лирования отношения принадлежности точек этой линии и это поверхности (рис.16.15, п.2.4).

Если секущая плоскость a занима-ет общее положение, то она пересекает вытянутый эллипсоид вращения по эл-липсу, отношения длин осей которого

зависит от положения этой плоскости

по отношению к его оси вращения.

В общем случае задача п.2.5 реша-ется с применением вспомогательных горизонтальных плоскостей уровня, а изобразительные свойства ортогональ-ных проекций получаемого эллипса описываются особенностями рис.12.46.

3. Параболоид вращения D явля -ется полуоткрытой поверхностью, система линейного каркаса которой оп-ределяется подсистемой конгруэнтных парабол-меридианов и конкурентных с ними подобных между собой паралле-лей-окружностей. Вид линии пересече-ния его плоскостью a зависит от её по-ложения по отношению к оси вращения поверхности.

3.1. Если секущая плоскость a па-раллельна оси i вращения поверхности, D, то она параллельна некоторому её меридиану, проходящему через эту ось, а поэтому линия m их пересече-ния подобна ему и является параболой (рис.16.15, п.п. 3.1,3.4).

3.2. Если секущая плоскость a пер-пендикулярна к оси i вращения поверх-ности D, то фигурой сечения является окружность m как одна из параллелей его линейного каркаса (рис.16.15 п.3.3).

3.3. Если секущая плоскость a пе-ресекает ось вращения поверхности под острым углом, то она пересекает все её меридианы и линией пересече-ния полуоткрытой поверхности явля-ется замкнутая линия – эллипс.

Если плоскость a занимает фронта-

льно-проецирующее положение, то её вырожденная проекция a₂ содержит в себе фронтальную проекцию m₂ иско-мой линии пересечения, а её горизон-тальная проекция m₁ строится на осно-ве графического моделирования отно-шения принадлежности точек линии m к поверхности параболоида.

Если секущая плоскость a занима-ет в пространстве общее положение и пересекает все меридианы параболо-ида, то искомой линией их пересечения

является эллипс общего положения.

Ортогональные проекции этого эл-липса строятся графически с помощью вспомогательных секущих горизонталь-ных плоскостей, которые пересекают поверхность по её параллелям, а пло-скость a - по её горизонталям. Пересе-

каясь, эти линии определяют проекции

искомой линии m пересечения плоско-сти a и поверхности D (рис.16.15,п. 3.5)

4. Однополостный гиперболоид вращения W является открытой пове-рхностью, образованной вращением либо гиперболы вокруг её мнимой оси, либо прямой линии, скрещивающейся с этой осью. Поэтому сечение этой пове-рхности плоскостью a, походящей че-рез ось, является меридиональной ги-перболой (рис.16.15. п.4.1), а сечение плоскостью, параллельной оси,- гипер-болой, которая родственна меридиана-льной гиперболе (п. 4.4).

Если плоскость a перпендикулярна к оси вращения поверхности W, то она пересекает её по окружности m как одной из параллелей её линейного кар-каса.

Если плоскость a пересекает ось под острым углом, то она пересекает все меридианы поверхности W и в ито-ге линией их пересечения является замкнутая кривая – эллипс (п. 4.2)

Если секущая плоскость занимает общее положение, то она также пере-секает всем меридианы поверхности W в точках эллипса m общего положения.

Ортогональные проекции этой линии строятся при помощи вспомогательных секущих плоскостей уровня, пересека-ющих поверхность W по её паралле-лям, а плоскость a - по её горизон-талям, которые, в свою очередь, пере-секаясь, определяют точки искомой ли-нии пересечения плоскости a и поверх-ности W.

О б щ и е в ы в о д ы и з р е ш е н и я

з а д а ч и 7.5

1. Если поверхность вращения с вертикальной осью любого вида пере-секается плоскостью частного поло-жения, то одна из ортогональных про-екций линии их пересечения совпадает с вырожденной проекцией секущей плоскости, а вторая строится на ос-нове графического моделирования от-ношения принадлежности точек этой линии к заданной поверхности.

2. Если секущая плоскость зани-мает в пространстве общее положе-ние, а ось пересекаемой поверхности

вертикальна, то для решения пози-ционой задачи на построение линии их

пересечения следует принимать та-кие вспомогательные секущие плоско-сти, которые пересекали бы данную поверхность по её параллелям.