U(x)V(x)- степенно-показательное выражение
1) y=U(x)V(x)= 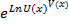 =
= 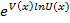
y’= 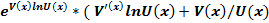 *U’(x)) - ф-ла Лейбница-Бернулли
*U’(x)) - ф-ла Лейбница-Бернулли
2) y=U(x)V(x)
z=lny
z’=1/y *y’
y’=y*z’
y’=y(lny)’
3) y=U(x)V(x)
y’ = U(x)V(x)* lnU(x)*V’(x)+V(x) U(x)(V(x)-1)U’(x)= U(x)V(x)(lnU(x)*V’(x)+ 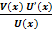 )
)
8*. Первый дифференциал. Инвариантность формы первого дифференциала.
 Если y=f(x) опреелена на X и непрерывна в токе xo∈X,
Если y=f(x) опреелена на X и непрерывна в токе xo∈X,
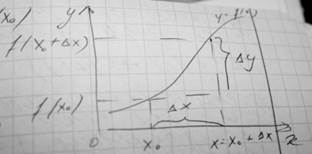
∆у= f(xo +∆x) – f(xo), xo +∆x∈ X
Если приращение ф-ии может быть представлено так: ∆y= A∆x+0(∆x), где A- некоторое число, независящее от ∆x, то ф-я f(x) называется дифференцированной в точке x0? А линейная часть этого выражения A∆x наз. Дифференциалом ф-ии в точке х0 и обозначается dy или df(x).
Для того, чтобы функция была дифференцируема, необходимо и достаточно, чтоб для нее в данной точке существовала конечная производная.
Геометрически дифференциал функции- это приращение ординаты касательной, проведенной к графику функции y=f(x) данной точки, когда xo получает приращение ∆x.
Инвариантность(неизменность):
y=f(x) 1) пусть x- независимая переменная dy=f'(x)dx=y’dy
2)пусть x-зависимая переменная, x=φ(t) y=f(φ(t))
dy= y’tdt= y’x*x’tdt=y’xdx
так dy= y’xdx
dx= x’tdt
Форма дифференциала может быть сохранена даже в том случае, если прежняя независимая переменная заменена новой.
 2015-05-13
2015-05-13 571
571








