
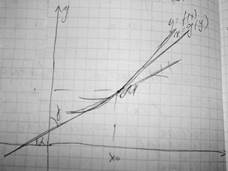
Касательная к кривой y(f) в точке M0(x0, f(x0)) – предельное положение секущей MN при неограниченном приближении N по кривой к M.
y-f(x0)= f’(x0)(x-x0) – ур-е касательной
Производная- это tg угла наклона (угл.коэфф) касательной к кривой y= f(x) в точке (x0;f(x0))
K=tgα= f’(x0), α-угол наклона касательной
 Нормаль к кривой y(f) в точке M0(x0, f(x0))- прямая, прохожящая через M и перпендикулярная касательной к кривой в этой точке.
Нормаль к кривой y(f) в точке M0(x0, f(x0))- прямая, прохожящая через M и перпендикулярная касательной к кривой в этой точке.
k2=1/k1
y-f(x0)= -1/ f’(x0) * (x-x0)
f’(x0) характеризует скорость изменения ф-ии f(x) в точке x0- мгновенная скорость.
3*. Правила вычисления производных с демонстрацией на конкретных примерах.
| № | Y=f(x) | Y’=f’(x) |
| C | ||
| xm | mxm-1 | |
| ax(0<a≠1) | axlna | |
| ex | ex | |
| logax (0<a≠1) | 1/x logae | |
| lnx | 1/x | |
| sinx | cosx | |
| cosx | -sinx | |
| tgx | 1/cos2x | |
| ctgx | -1/sin2x | |
| arcsinx | 1/√1-x2 | |
| arccosx | -1/√1-x2 | |
| arctgx | 1/1+x2 | |
| arcctgx | -1/1+x2 | |
| √x | 1/2√x |
1)(CU)’= C*U’
2)(U±V)’= U’±V’
3)(UV)’=U’V+UV’
4)(U/V)=U’V-UV’ / V2
4*. Производная сложной функции с демонстрацией на конкретных примерах.
Если функция u=f(x) имеет в некоторой точке x производную (∃u'x=u’(x))
Если y=f(u) имеет в соответствующей точке u производную (∃y’u= f’(u))
то y = f(u(x))в точке х также будет иметь производную, равную произведению производной u’(х) и y'(u) ф-й f(u) и u(x).
Y'x= y’u*u’x
 5. Производная обратной функции с демонстрацией на конкретных примерах.
5. Производная обратной функции с демонстрацией на конкретных примерах.
Пусть
1) Ф-я f(x) в точке x= x0 имеет конечную и отличную от нуля производную ∃f'(x0)≠0
2) Для нее существует однозначная обратная ф-я ∃x=g(y), непрерывная в соответствующей точке y=y0, где y0=f(x0)
Тогда ∃ g'(y0) = 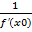
y’x= 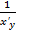 x’y=
x’y= 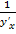 f’(x0)=tgα, α- угол наклона кас. к ОХ;
f’(x0)=tgα, α- угол наклона кас. к ОХ;
g’(y0)=tgβ, β- угол наклона кас. к ОY
α +β=П/2, tgβ=1/ tgα
Пр. y= 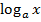 , y'x=?. ∃x=
, y'x=?. ∃x= 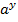 , x’y=
, x’y= 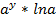 , y'x=1/ x’y=1/
, y'x=1/ x’y=1/ 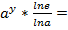 1/x*
1/x* 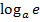 .
.
 2015-05-13
2015-05-13 455
455







