Основные понятия. Определение.Комплексным числом называют выражение вида

Определение. Комплексным числом 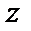называют выражение вида ,

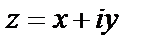где 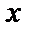и 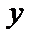– действительные числ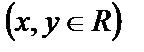а , а 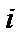– мнимая единица 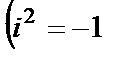или .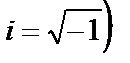

Число 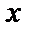называют действительной частью комплексного числа 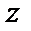и обозначают 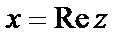, а число 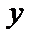– мнимой частью числа 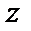и обозначают .

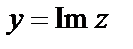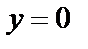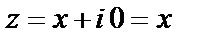Если , то – это число совпадает с действительным числом.

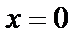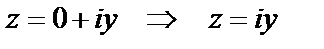Если , то – это число называется чисто мнимым.

Определение. Число 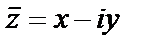называется сопряженным с числом .

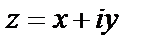Таким образом .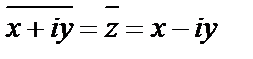

Каждое комплексное число 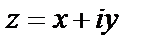можно изобразить геометрически точкой с координатами 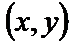на плоскости 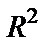(в декартовой прямоугольной системе координат), либо радиус-вектором этой точки.

y

x

z

y

Рис. 1

Определение. Плоскость, на которой изображены комплексные числа называется комплексной плоскостью и обозначается . (рис.1)

x

В дальнейшем будем отождествлять комплексные числа и точки на (ось ОX – действительная ось, OY – мнимая ось).

Определение. Расстояние от начала координат до точки 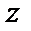называют модулем комплексного числа :

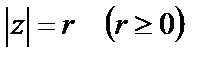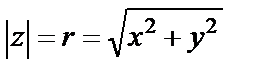(1)

Определение. Аргументом комплексного числа называют угол 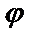между радиус-вектором точки 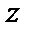и положительным направлением оси .

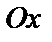Аргумент комплексного числа определяется с точностью до слагаемого .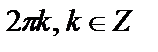

Значение аргумента, удовлетворяющее условию 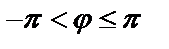называют главным и обозначают 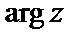, а множество всех значений аргумента .

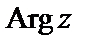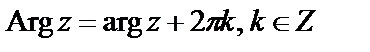(2)

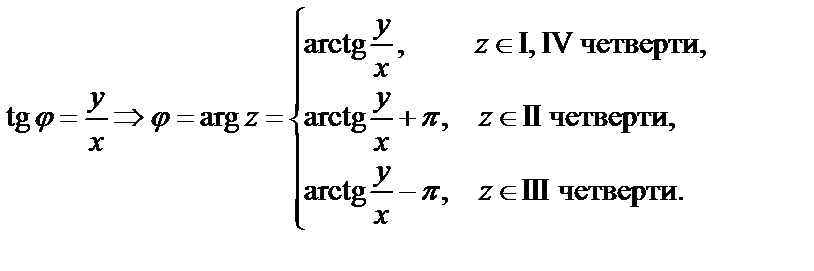(3)

Имеем , , .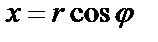

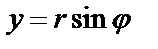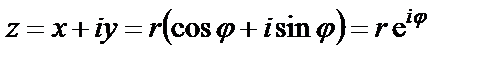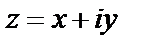– алгебраическая форма,

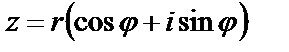– тригонометрическая форма,

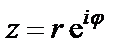– показательная форма.