2015-05-13
3433
Определение. Уравнение вида
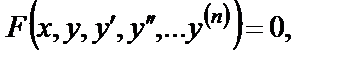(7)
связывающее независимую переменную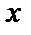 
, неизвестную функцию 
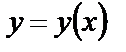и ее производные 
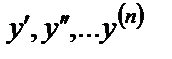называют дифференциальным уравнением n -го порядка.
Определение. Уравнение вида
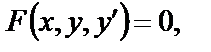(8)
связывающее независимую переменную 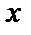, неизвестную функцию 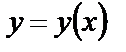и ее производную 
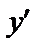называется дифференциальным уравнением первого порядка.
Порядком дифференциального уравнения называют порядок старшей производной, входящей в это уравнение.
Определение. Общим решением дифференциального уравнения (2) в области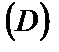 
называют функцию 
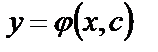, где с – произвольная постоянная, удовлетворяющая следующим условиям:
1) для каждого числа с функция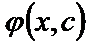 
является решением уравнения (2);
2) если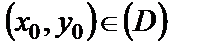 
, то существует такое число 
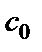, что решение 
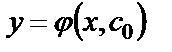удовлетворяет начальному условию 
.
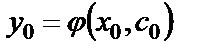Если общее решение получено в неявном виде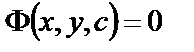 
, то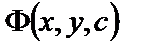 
называют общим интегралом, а 
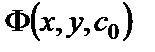– частным интегралом уравнения (8).
Если дифференциальное уравнение (8) можно разрешить относительно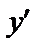 
, то оно примет вид:
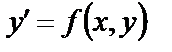(9)
Дифференциальное уравнение (9) называют разрешенным относительно производной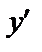 
.
Уравнение (9) записывают иногда в виде:
,
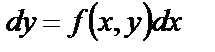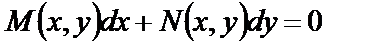, (10)
где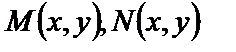 
– функции двух переменных.
Теорема Коши. (Теорема существования и единственности решения дифференциального уравнения (9)). Если в уравнении (9) функция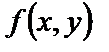 
и ее частная производная по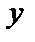 
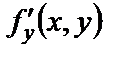определены и непрерывны в области 
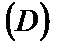плоскости (XOY) и 
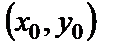– произвольная точка из 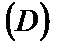, то существует, причем единственное, решение этого уравнения 
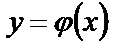, удовлетворяющее начальному условию 
.
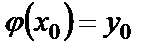Задачу нахождения решения уравнения (9) с заданным начальным условием называют задачей Коши.
Определение. Частным решением дифференциального уравнения (9) называют любую функцию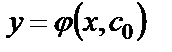 
, которая получается из общего решения, если произвольной постоянной 
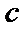придать определенное значение 
.
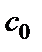Определение. Дифференциальное уравнение I порядка называют уравнением с разделяющимися переменными, если его можно записать в виде
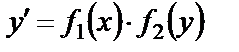(11)
или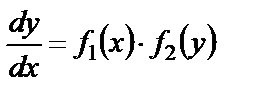 
или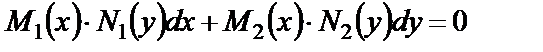 
, (12)
где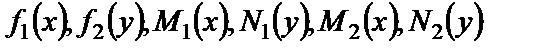 
– заданные функции.
Для решения уравнения (11) разделим переменные:
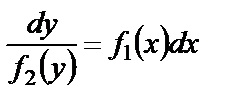
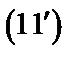
Или разделим обе части (12) на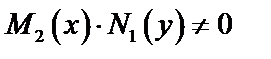 
:
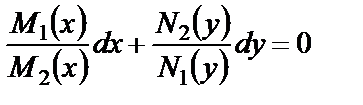, (13)
откуда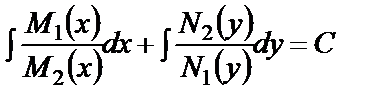 
Определение. Уравнение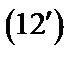 
или (13) называют уравнением с разделенными переменными.
Определение. Функция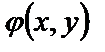 
называется однородной функцией нулевого измерения, если она зависит только от отношения 
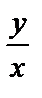, т.е. 
.
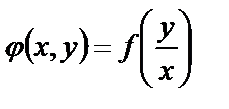Определение. Однородным дифференциальным уравнением называется уравнение вида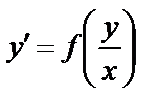 
(14)
Введем новую неизвестную функцию, положив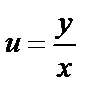 
, или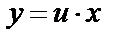 
. Дифференцируя, получим 
.
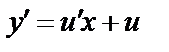Подставим в уравнение (14), преобразуем его к виду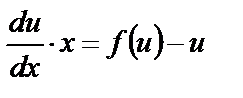 
. Разделяя переменные и интегрируя, найдем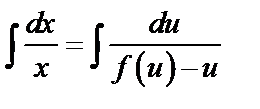 
или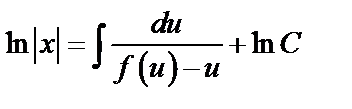 
Отсюда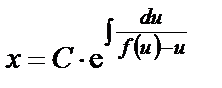 
.
После выполнения интегрирования нужно вернуться к функции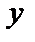 
, положив .
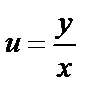Пример. Решить уравнение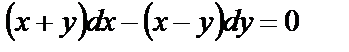 
.
Выражая производную, получим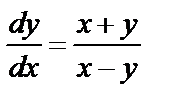 
или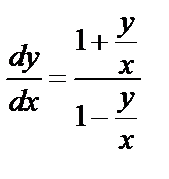 
.
Положим 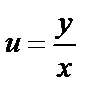. Тогда , 
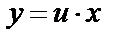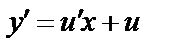. Подставив в уравнение, получаем 
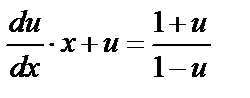. Откуда 
.
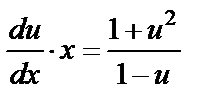Разделим переменные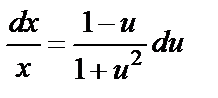 
.
После интегрирования находим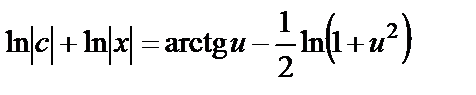 
или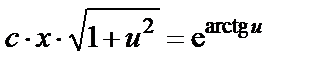 
.
Окончательно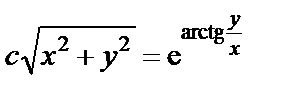 
.
Определение. Линейным дифференциальным уравнением называется уравнение вида
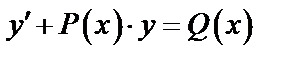(15)
Введем две новые неизвестные функци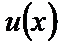и 
и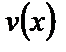 
, положив 
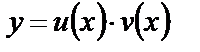. Поскольку неизвестных функций стало две, а условий на эти функции только одно (их произведение должно удовлетворять уравнению (15)), то еще одно условие на эти функции мы можем наложить произвольно, чем мы и воспользуемся ниже.
Подставим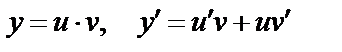 
в (15),
получим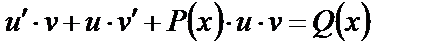 
или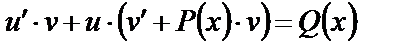 
(16)
В качестве функции 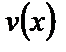выберем любую функцию, удовлетворяющую условию 
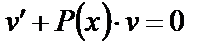. (17)
Получим уравнение с разделяющимися переменными для нахождения 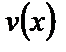. Проинтегрируем это уравнение, полагая постоянную интегрирования равной нулю (последнее законно, так как нас устраивает любое решение уравнения (17)):
,
,
,
.
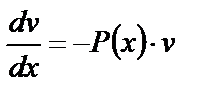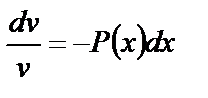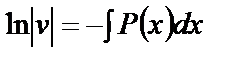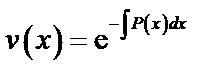Подставим найденное значение 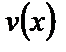в уравнение (16):
,
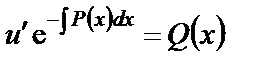откуда
.
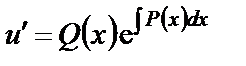Интегрируя, найдем функцию :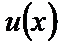 
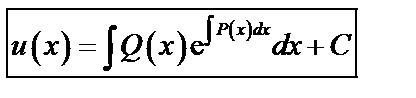. Перемножив найденные функци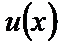и и 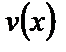, получим общее решение уравнения (15).
Определение. Уравнением Бернулли называется уравнение вида
,
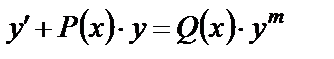где m – любое действительное число. Решается это уравнение с помощью того же приема, что и линейное уравнение.
Определение. Уравнение
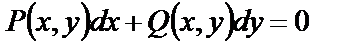(18)
называется уравнением полного дифференциала, если его левая часть представляет собой полный дифференциал некоторой функции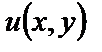 
. В этом случае уравнение (18) можно переписать в виде 
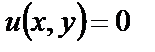. Общий интеграл уравнения (18) будет
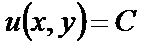. (19)
Теорема. Пусть функции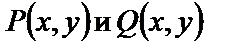 
имеют непрерывные частные производные в некоторой области (D) плоскости (XOY). Для того, чтобы выражение 
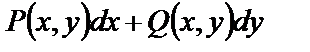было полным дифференциалом некоторой функции 
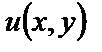, необходимо и достаточно, чтобы во всех точках области (D) выполнялось равенство
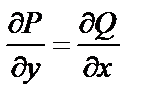. (20)
Пусть дано уравнение (18), для которого выполняется условие (20). Последнее означает, что существует функция 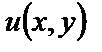такая, что
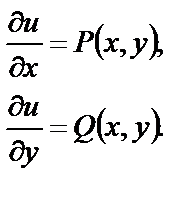(21)
Чтобы решить уравнение (18), нужно, исходя из равенств (21), найти функцию 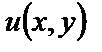и записать общий интеграл уравнения (18) в форме (19).
Пример. Найти решение уравнения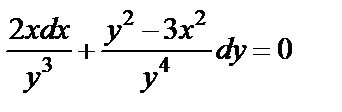 
, удовлетворяющее условию 
.
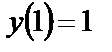Имеем: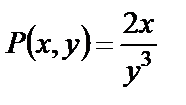 
, 
.
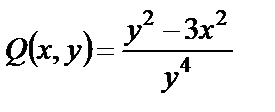Найдем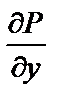 
и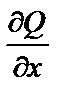 
: 
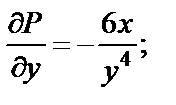
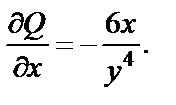
Таким образом,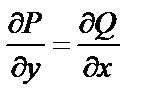 
, т.е. существует такая функция 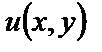, что
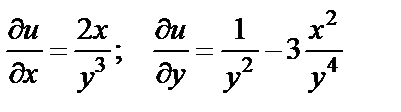(22)
Для нахождения 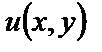проинтегрируем по x первое из равенств (22):
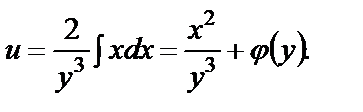(23)
Здесь неизвестная функция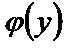 
играет роль постоянной интегрирования. Для нахождения 
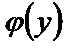продифференцируем (23) по y:
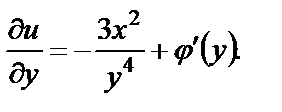
С другой стороны, из (22) имеем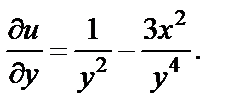 
Из этих двух равенств получаем 
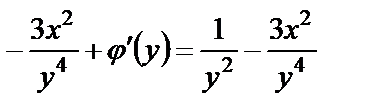или 
.
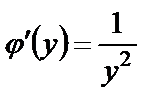Отсюда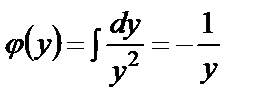 
. (24)
Подставляя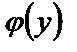 
в (24), получаем, согласно (19), общий интеграл данного уравнения в виде 
.
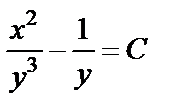Замечание. Так как, согласно (19), функция 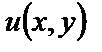приравнивается произвольной постоянной, то при выполнении интегрирования (24) постоянную интегрирования можно не писать.
