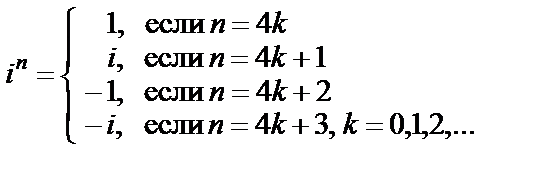 (6)
(6)
Пример 1. 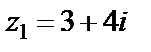 – вершина квадрата, лежащая на окружности
– вершина квадрата, лежащая на окружности 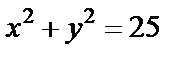 . Найти остальные вершины.
. Найти остальные вершины.
Решение: Имеем
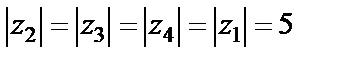
Т.к. 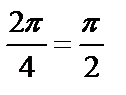 , то достаточно повернуть
, то достаточно повернуть 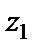 на угол
на угол 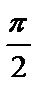 последовательно три раза. Тогда
последовательно три раза. Тогда
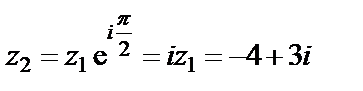
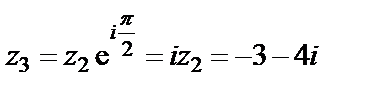
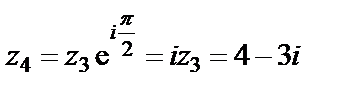 .
.
Пример 2. Вычислить 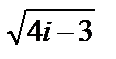 .
.
Решение:
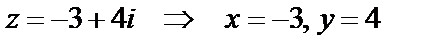 .
.
Т.к 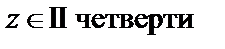 , то
, то 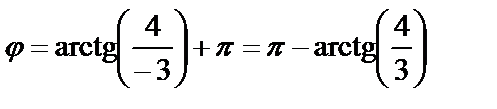 .
.
Т.е. 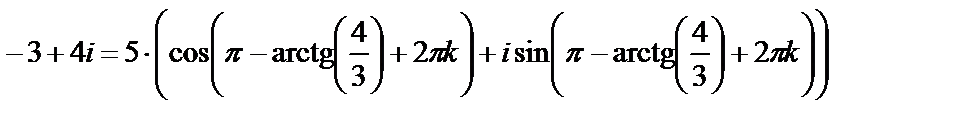 =
=
= 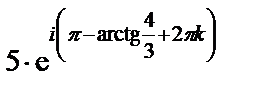 .
.
Имеем 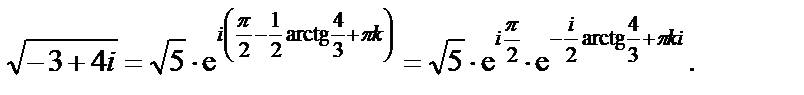
Т.к. 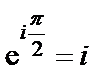 , то
, то 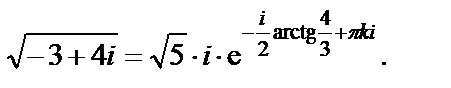
При 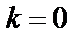
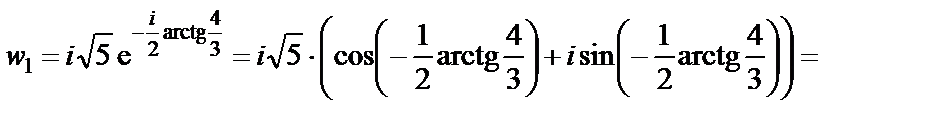
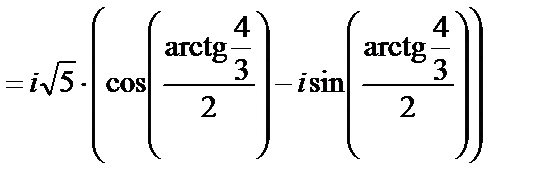
Используем формулы:
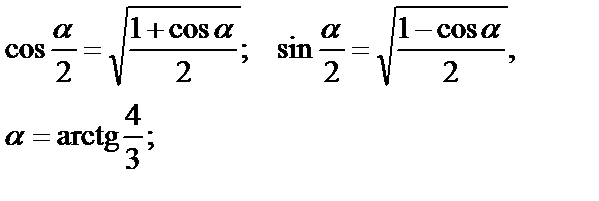
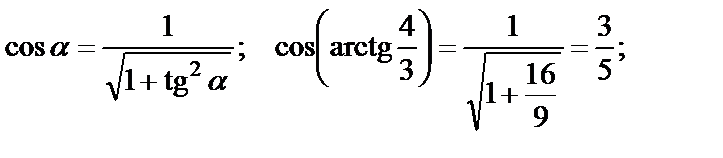
Тогда 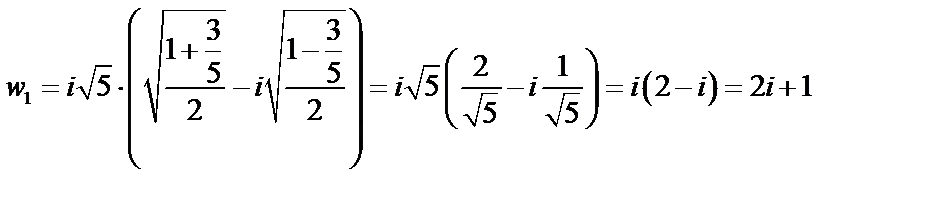 .
.
Таким образом, 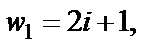
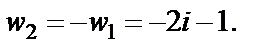
Пример 3. Вычислить 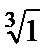 .
.
Решение:
Имеем 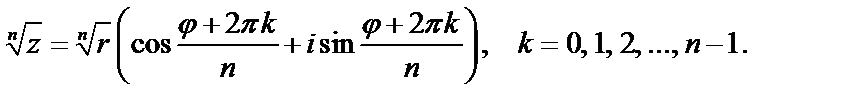
Тогда 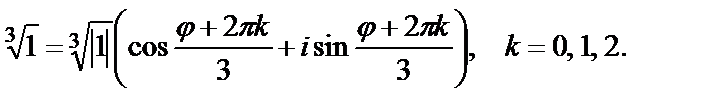
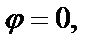
т.е.
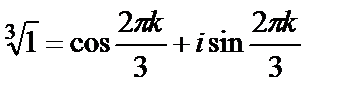
,
при 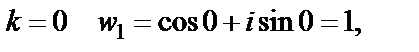
при 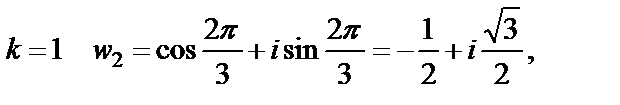
при 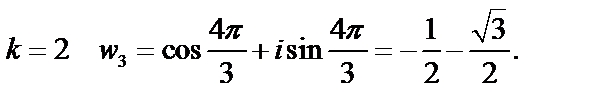
Таким образом,
![]()
Если корни 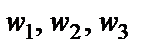 , лежащие на окружности соединить отрезками, то получим правильный треугольник.
, лежащие на окружности соединить отрезками, то получим правильный треугольник.
Глава 2. Дифференциальные уравнения
Дифференциальные уравнения первого порядка.
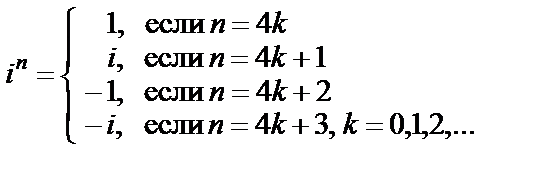 (6)
(6)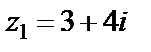 – вершина квадрата, лежащая на окружности
– вершина квадрата, лежащая на окружности 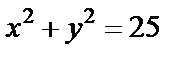 . Найти остальные вершины.
. Найти остальные вершины.
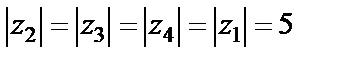
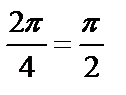 , то достаточно повернуть
, то достаточно повернуть 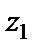 на угол
на угол 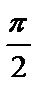 последовательно три раза. Тогда
последовательно три раза. Тогда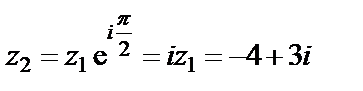
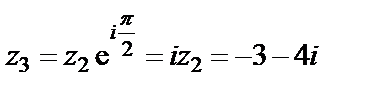
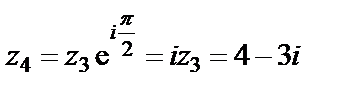 .
.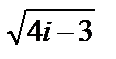 .
.
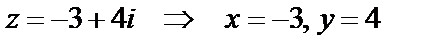 .
.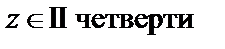 , то
, то 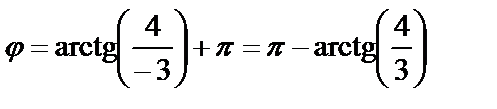 .
.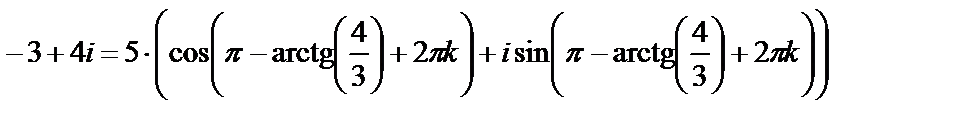 =
=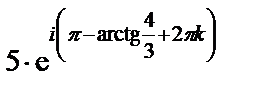 .
.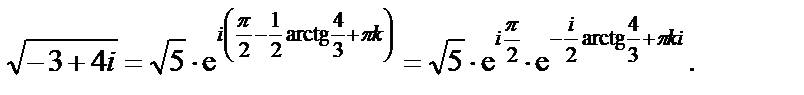
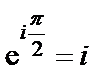 , то
, то 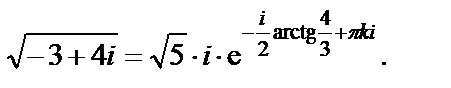
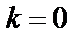
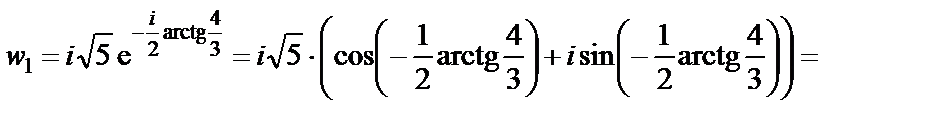
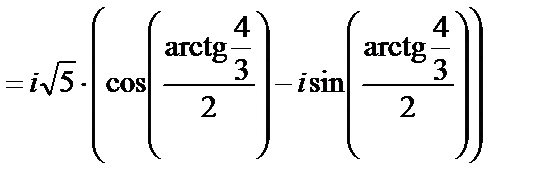
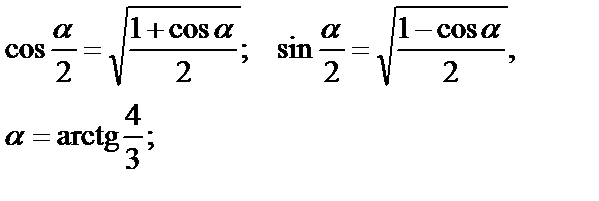
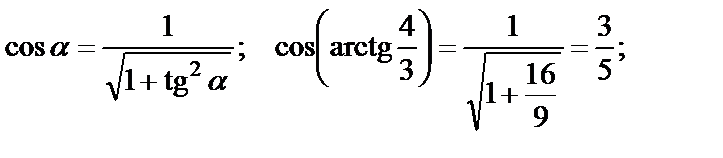
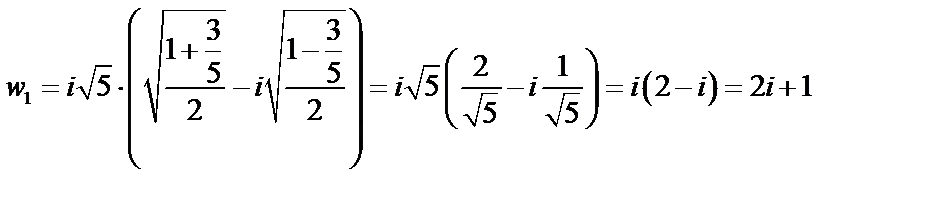 .
.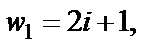
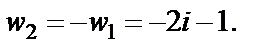

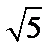
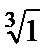 .
.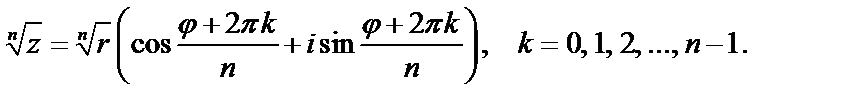
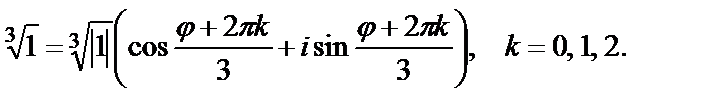

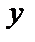
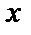
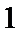
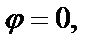 т.е.
т.е. 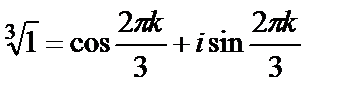 ,
,
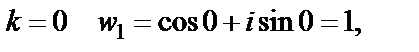
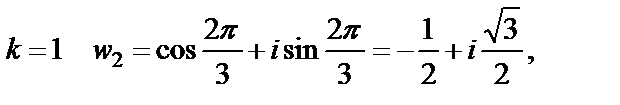
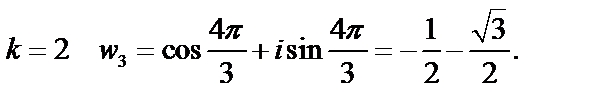

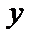
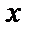
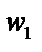
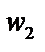
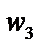
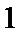
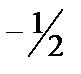
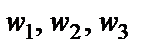 , лежащие на окружности соединить отрезками, то получим правильный треугольник.
, лежащие на окружности соединить отрезками, то получим правильный треугольник. 2015-05-13
2015-05-13 381
381








