Дано дифференциальное уравнение второго порядка
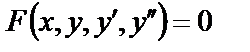 (25)
(25)
Рассмотрим два частных случая, когда интегрирование уравнения (25) может быть сведено к интегрированию дифференциального уравнения первого порядка.
1. Уравнение (25) не содержит в явном виде неизвестную функцию, т.е. имеет вид
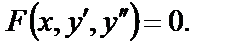 (26)
(26)
Введем новую неизвестную функцию 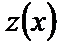 , положив
, положив 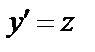 . Тогда
. Тогда 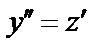 и уравнение (26) принимает вид
и уравнение (26) принимает вид
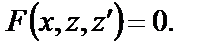
Предположим, что нам удалось найти общее решение этого уравнения 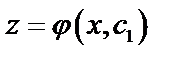 .
.
Сделав обратную замену, получим 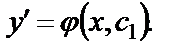 Проинтегрировав последнее равенство, найдем общее решение уравнения (26):
Проинтегрировав последнее равенство, найдем общее решение уравнения (26):
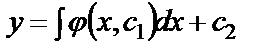
Пример. Решить уравнение 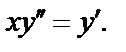 (27)
(27)
Решение:
Пусть 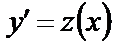 , тогда
, тогда 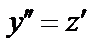 и после замены уравнение (27) примет вид
и после замены уравнение (27) примет вид 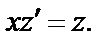 Получили уравнение с разделяющимися переменными, которое решается стандартным методом:
Получили уравнение с разделяющимися переменными, которое решается стандартным методом:
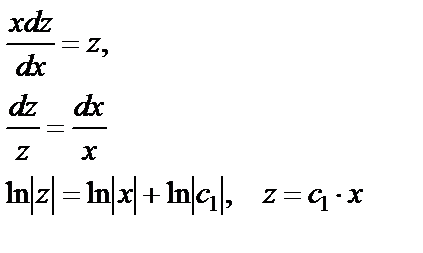
После обратной замены получаем: 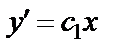 ,
, 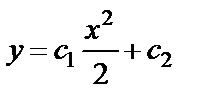 – общее решение уравнения (27).
– общее решение уравнения (27).
2. Уравнение (25) не содержит в явном виде неизвестную переменную, т.е. имеет вид
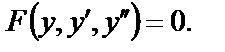 (28)
(28)
Введем новую неизвестную функцию 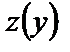 , положив
, положив 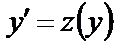 . Продифференцируем это равенство
. Продифференцируем это равенство 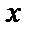 , используя правило дифференцирования сложной функции:
, используя правило дифференцирования сложной функции:
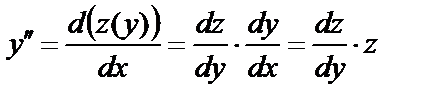 .
.
После замены уравнение (28) примет вид 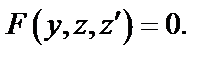 Получили уравнение первого порядка. Общее решение этого уравнения будет иметь вид
Получили уравнение первого порядка. Общее решение этого уравнения будет иметь вид 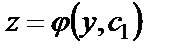 . Возвращаясь к функции y, получим
. Возвращаясь к функции y, получим 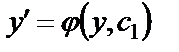 или
или 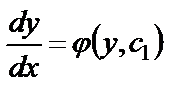 .
.
Разделив перменные и проинтегрировав, найдем общий интеграл уравнения (28) в виде
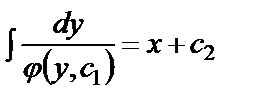 .
.
Пример. Решить уравнение 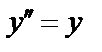 . (29)
. (29)
Пусть 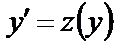 , тогда
, тогда 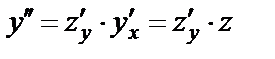 . Подставив в (29), получим:
. Подставив в (29), получим: 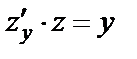 ,
, 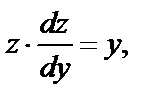
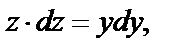
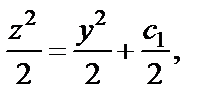
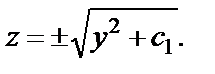
Отсюда 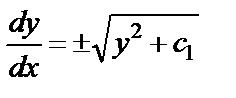 или
или 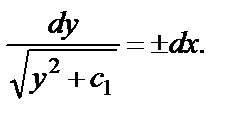 Интегрируя, получаем
Интегрируя, получаем 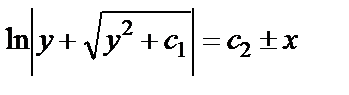 .
.
 2015-05-13
2015-05-13 475
475








