Определение. Уравнение
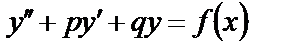 (36)
(36)
называют линейным диффернциальным уравнением со специальной правой частью, если
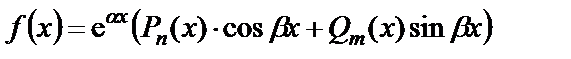 , (37)
, (37)
где 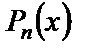 ,
, 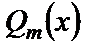 – многочлены степеней n и m соответственно,
– многочлены степеней n и m соответственно, 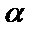 и
и 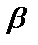 – действительные числа.
– действительные числа.
Будем искать частное решение уравнения (36) в виде:
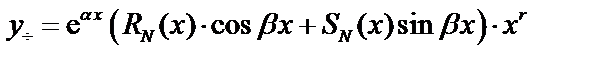 , (38)
, (38)
где 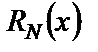 и
и 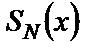 многочлены степени N с неопределенными коэффициентами,
многочлены степени N с неопределенными коэффициентами, 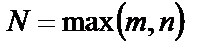 , а показатель степени r – число корней характеристического уравнения равных
, а показатель степени r – число корней характеристического уравнения равных 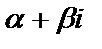 .
.
Теорема. Общее решение линейного неоднородного уравнения (36) складывается из общего решения соответствующего однородного уравнения 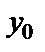 и какого-либо частного решения данного неоднородного уравнения
и какого-либо частного решения данного неоднородного уравнения 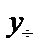 , т.е.
, т.е.
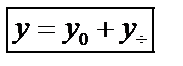 (39)
(39)
Пример. Найти общее решение уравнения 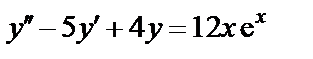
Решение.
1. Найдем 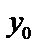 . Характеристическое уравнение:
. Характеристическое уравнение: 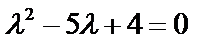
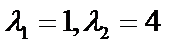
 (по формуле 33)
(по формуле 33) 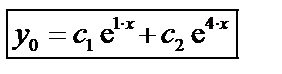 .
.
2. Найдем 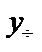 .
.
Имеем 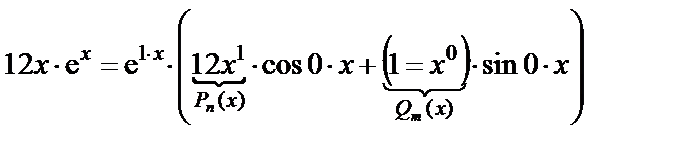 ,
,
т.е. 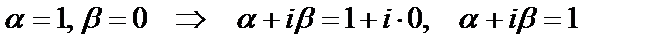 – корень первой кратности характеристического уравнения (т.е. r = 1, т.к.
– корень первой кратности характеристического уравнения (т.е. r = 1, т.к. 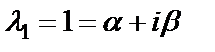 ). Находим
). Находим 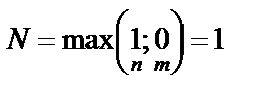 , следовательно, по (38)
, следовательно, по (38) 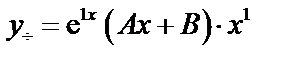 . Найдем А, В.
. Найдем А, В. 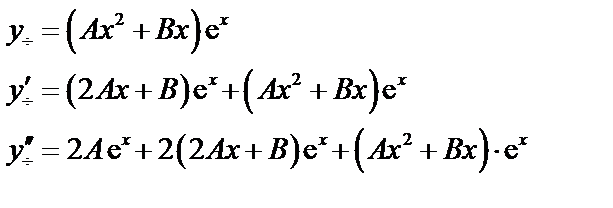
Подставим 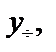
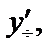
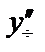 в уравнение
в уравнение 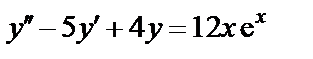 .
.
Получим 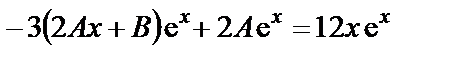
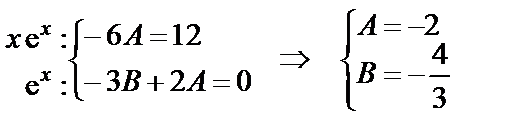
Следовательно, 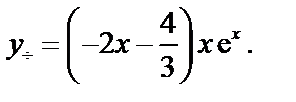
Ответ: 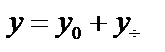 ,
, 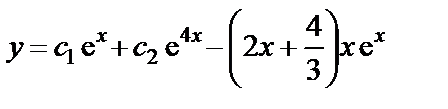 .
.
 2015-05-13
2015-05-13 417
417








